3/71 Kurs maturalny rozszerzenie
Podaj ilość rozwiązań równania f(x) = p w zależności od parametru p, gdzie (6 pkt):
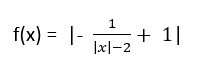
oraz narysuj funkcję y = f(p), która parametrowi „p” przyporządkowuje ilość rozwiązań równania f(x) =p.
Hej! Jak ugryźć zadanie 3? Zrobiłem przekształcenia, doszedłem do ostatecznej formy tylko jest jedno ale... brakuje tych dwóch prostych które biegną między asymptotami pionowymi -2 i 2, tych które idą w górę wzdłuż osi y, mam te dwie boczne wzdłuż asymptop lecz brakuje mi tych środkowych..
Matematyka Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Zrobiłem taką kolejnośc: 1/x przesuniecie o wektor [2,0] --> 1/x-2 potem zrobiłem symetrie soy* aby mieć moduł w mianowniku wiec mialem 1/|x|-2 i teraz dopiero zrobiłem symetrie -f(x) , być może gdzieś tutaj jest bład a ja go nie zauważyłem
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Najlepiej zacząć od przekształcenia - f(x) a następnie przesunąć o wektor [2,1], potem dopiero zastosować wartości bezwzględne. Mała szansa że gdzieś się pomylisz :)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A jak zrobić drugą część tego zadania?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@x, Pierw musisz narysować wykres, i twoim p jest jakaś liczba czyli prosta równoległa z osią ox, zatem gdy tą prostą przyłożysz do wykresu i dotyka się z 3 punktami wykresu to masz tam 3 rozwiązania
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Najważniejsze tu jest kolejność 2 pierwszych przekształceń, czyli wektorów i - f(x), bo Jexeli najpierw dajesz - f(x) to potem dajesz wektor [x, y], a jeżeli najpierw wektor to potem minus zmieni ci znak więc musisz przesunąć o [-x, y]