Grzegorz.p7 713 wyśw. 15-10-2020 01:03

Kiełbasa 376/71

Wyznacz te wartości parametru m, dla których równanie (x^2 - 2x + m -2)(|x-1| -m +1) = 0 ma dokładnie trzy pierwiastki rzeczywiste? Oblicz te pierwiastki. 

Rozwiązałem owe zadanie sposobem graficznym. Ale jestem ciekawy czy można je obliczyć sposobem pisemnym, coś tam zacząłem ale nie wiem czy to się wszystko trzyma.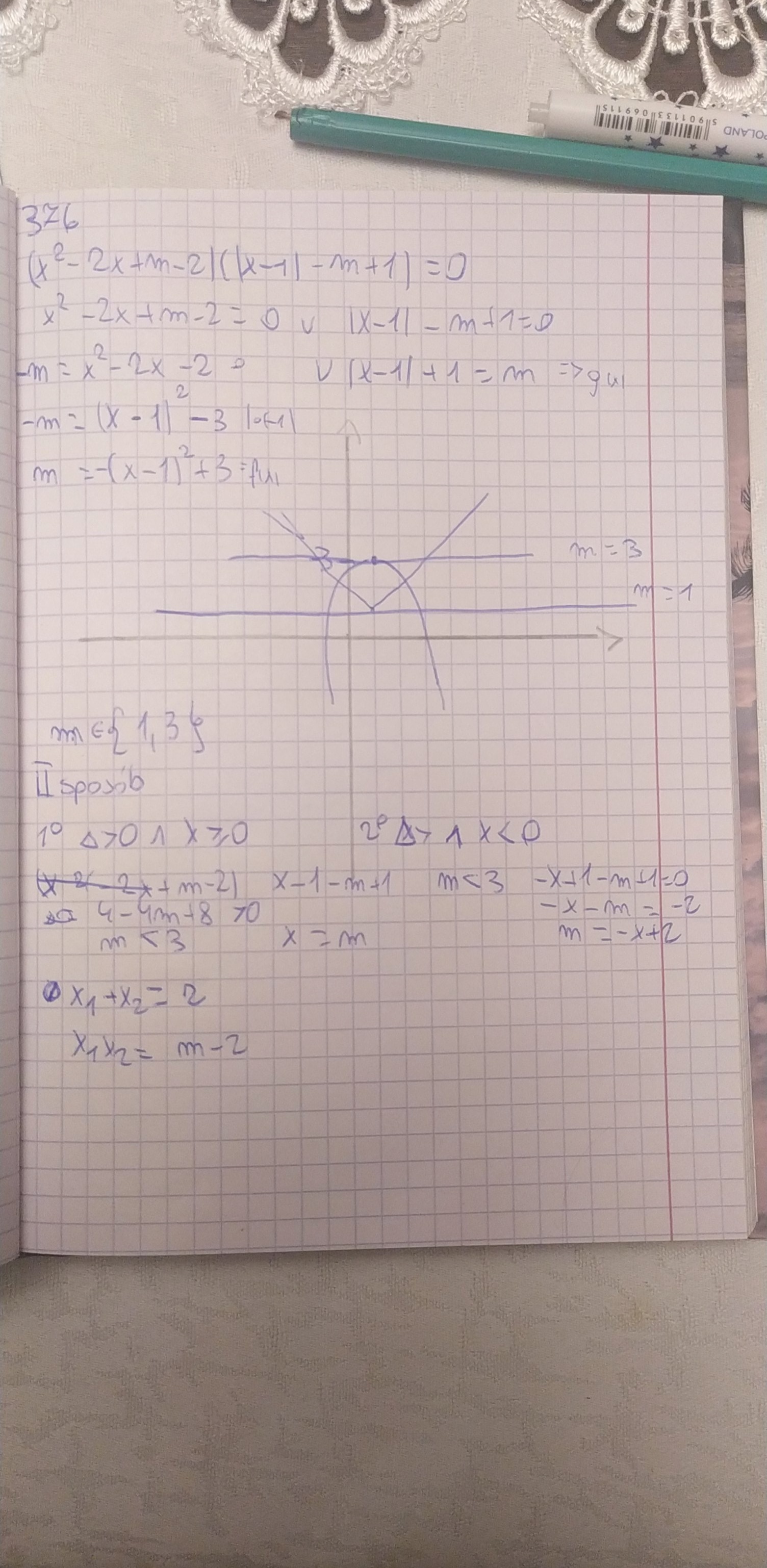 

Wielomiany Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski 04-11-2020 16:31

To jest typowe zadanie gdzie głównym sposobem (a czasem jedynym ze względu na zawiłość obliczeń) jest sposób graficzny. Jest tak dlatego, że każdy czynnik zależy od parametru m. Odpowiadając zatem na pytanie robiąc to innym sposobem po prostu nie ma sensu.