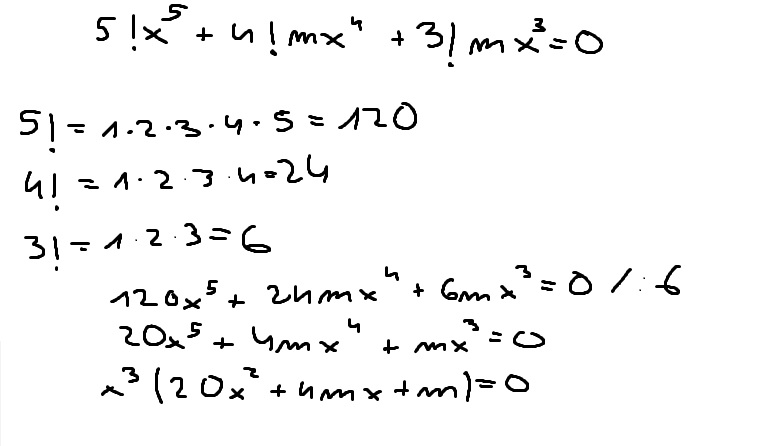Xvenusssx 942 wyśw. 15-10-2020 23:51

1b/75 kurs maturalny rozszerzony

Dla jakich wartości parametru m: równanie 5!x^5+4!mx^4+3!mx^3=0 posiada co najmniej 2 różne pierwiastki?

Jak się zabrać za ten przykład? Mógłby mi to ktoś rozpisać jak to na początku przekształcić do prostszej postaci?
wielomiany matematyka zadanie domowe Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
... 04-11-2020 16:31


Xvenusssx 04-11-2020 16:31

Dziękuję bardzo :)

Xvenusssx 04-11-2020 16:31

A co tym w zadaniu daje mi drugi warunek, czyli delta równa 0 i x0 różny od 0? Co z tego wynika?

Adam_Koz01 04-11-2020 16:31

Po wyciągnięciu x^3 przed nawias już znasz jedno rozwiązanie (jest ono potrójne, ale masz znaleźć co najmniej 2 różne).  Teraz musisz z równania kwadratowego znaleźć albo dwa rozwiązania (delta > 0, będziesz ich mieć 3 lub 2 jeśli jedno będzie równe zero), albo jedno rozwiązanie funkcji kwadratowej (delta = 0, dostaniesz jedno rozwiązanie, ale dodatkowym warunkiem jest x=/=0, bo tylko wtedy będziesz mieć dwa różne rozwiązania).

mariajurka 16-10-2024 15:11

skąd bierze się drugi warunek?