w 990 wyśw. 22-10-2020 20:56

5/76 kurs maturalny rozszerzony

Wyznacz wszystkie wartości parametru "k" dla których równanie (sinx-cosx)(sinx+0,5k)=0 ma w przedziale <0,3pi/2> dokładnie 4 różne rozwiązania. 

Czemu w zbiorze rozwiązań -0,5k∈<0,1) zero jest domknięte?

trygonometria Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
... 04-11-2020 16:31


Użytkownik nieznany 04-11-2020 16:31

Czemu nie odrzucamy też -Pierwiastek z2/2 ???


edit bo nie widzę kasacji kom    aaa bo tu jest jedno rozw dla sinx

wikusiak00 12-01-2021 00:40
Ja nie wiem dlaczego nie wyrzucamy tez -pier 2/2 ?
wikusiak00 12-01-2021 00:40
Ja nie wiem dlaczego nie wyrzucamy tez -pier 2/2 ?
... 12-01-2021 00:51

Skąd nie wyrzucamy -pierw z 2?

... 12-01-2021 01:12


wikusiak00 12-01-2021 15:38

z ostatecznej prawie odpowiedzi wyrzucamy pierw2/2 i moje pytanie brzmi dlaczego nie wyrzucamy również -pierw2/2 czyli wart dla 5/4 pi ? :)


... 12-01-2021 22:23

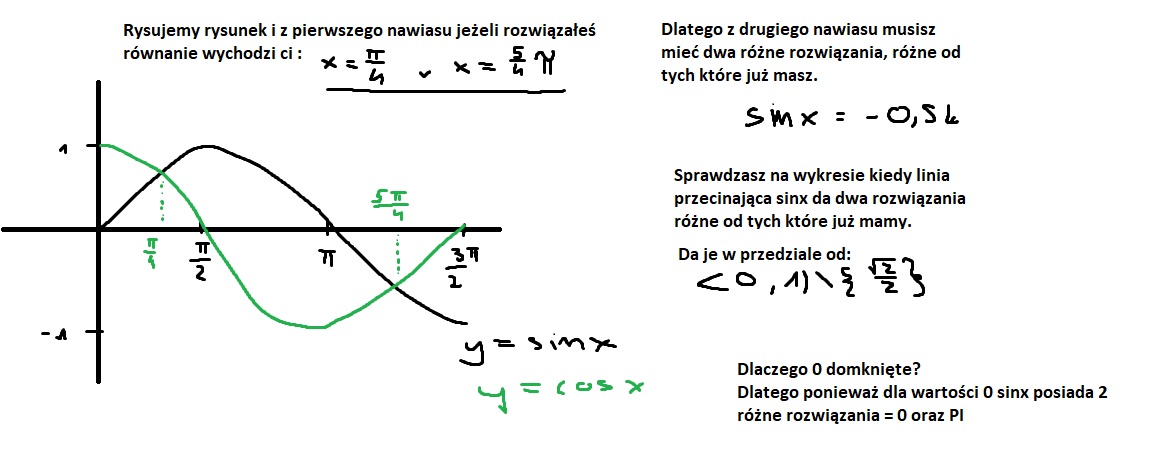
Otóż nie wyrzucamy jej ponieważ nie mamy z czego jej wyrzucić.

Narysowałem powyżej wykres ( TEN NA ZIELONO).

Ustalasz DLA JAKICH WARTOŚCI funkcja ta ma dwa różne rozwiązania. 

A więc zastanawiasz się kiedy linia pozioma przecinająca ten wykres przetnie go w dwóch punktach. 

Przetnie go dla wartości od <0, pierwiastek z 2/2) oraz (pierwiastek z 2 przez 2; 1).

Tylko wtedy. Zatem nie musimy wyrzucać z tego przedziału wartości -pierwiastek z 2 przez 2 ponieważ ta wartość nie należy do przedziału który rozpatrujemy.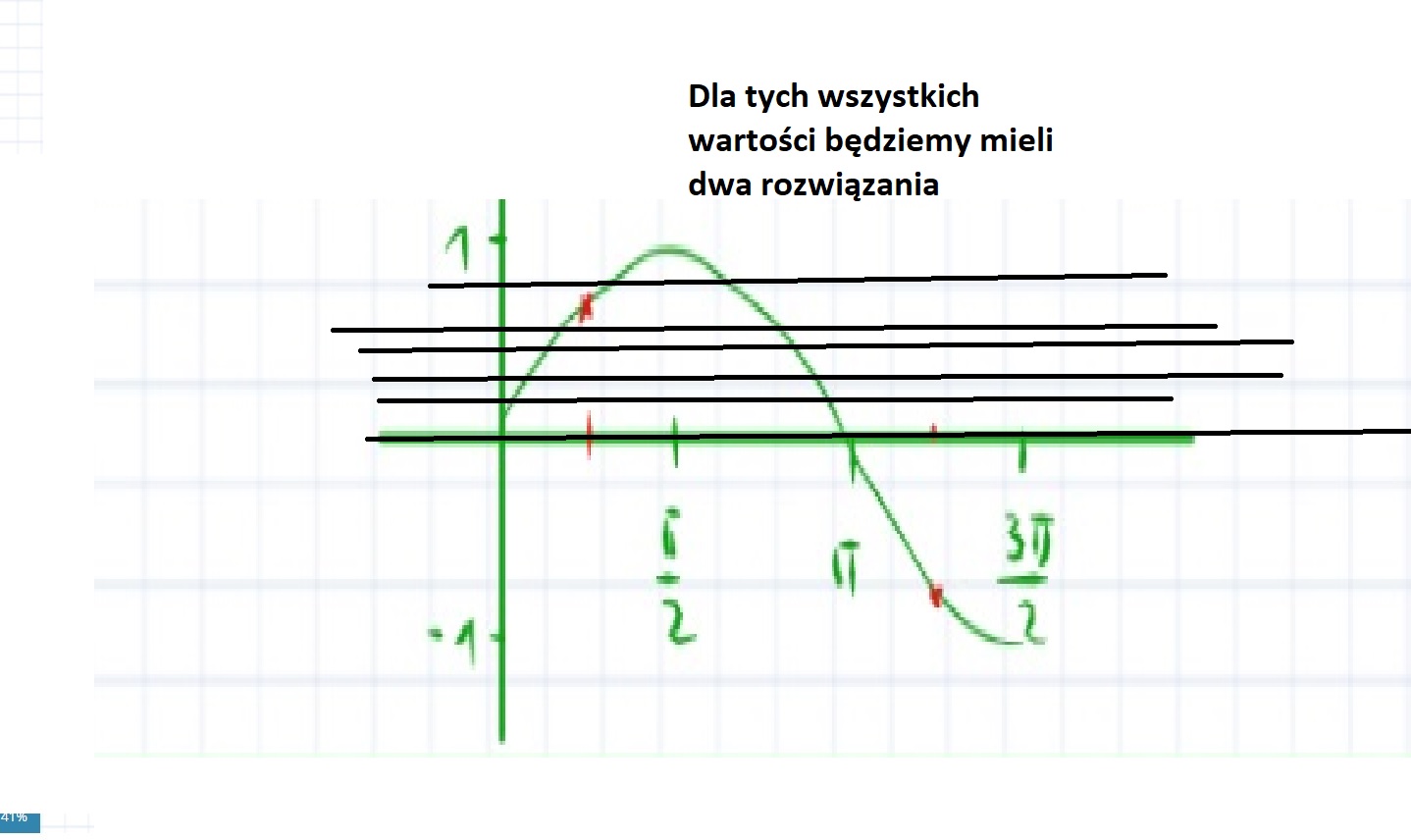

wikusiak00 13-01-2021 16:58

Nie wyświetlił mi się wcześniejszy wykres, już wszystko jest jasne dziękuję!!