Grzegorz.p7 1073 wyśw. 24-10-2020 15:21

1c/76 kurs maturalny rozszerzony

Podaj zbiór wartości funkcji, sin^4x - cos^4x

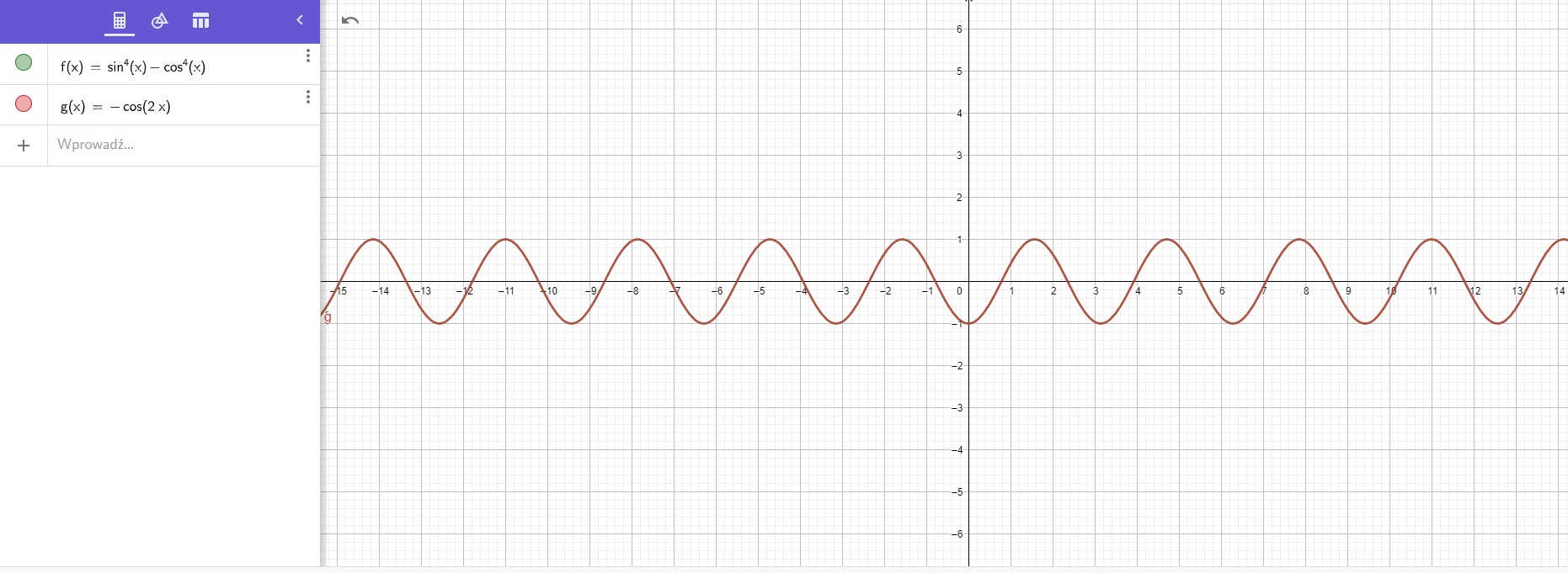
Przedstawiłem tą funkcje jako wzór skróconego mnożenia, czyli (sin^2x - cos^2x)(sin^2x + cos^2x) = (sin^2x - cos^2x)*1=

sin^2x - cos^2x = -(cos^2x - sin^2x) = -cos2x. więc zbiór wartości to <-1,1>. Jest to trochę inny sposób niż w odpowiedziach, ale chyba w pełni poprawny, i nie trzeba dawać żadnych założeń, więc mogę sobie przyznać 3 punkty?


trygonometria Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
... 04-11-2020 16:31

Jak widać na poniższym wykresie, wykres początkowy i twoje przekształcenie pokrywają się zatem przekształcenie jest jak najbardziej poprawne. Zbiór wartości jest również poprawny zatem jak najbardziej możesz sobie przyznać fulla za to zadanie.