1/77 cz.I kurs maturalny

Może mi ktoś powiedzieć co źle robię w podpunkcie b?
Matematyka trygonometria praca domowa Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jak rozwiązać dalej przykład „j”?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
w przykładzie b, powinieneś podzielić przez dwa i otrzymujesz cos^2x > 1 czyli:
cosx > pierwiastek z dwóch/2 lub cosx < -pierwiastek z dwóch/2 i rozwiazujesz, jesli chcesz to robic twoim sposobem to zrobiłeś błąd przy przy pierwiastkowaniu bo to wychodzi wtedy |sinx| < 1/2 czyli rozbijasz na dwa przypadki wieksze badz mniejsze od zera
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
w przykładzie j musisz pomnozysz razy 1/2 wtedy dostaniesz 1/2*sinx + pierwiastek z 3/2*cosx = 1/2 czyli:
sin(pi/6)*sinx + cos(pi/6)*cosx =1/2 ----> cos(x - pi/6) i z tego rozwiązujesz równanie
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Chodzi mi właśnie o to jak przejść do cos(x-pi/6)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
jest to wzór z tablic maturalnych z strony 16 "Funkcje sumy i różnicy kątów" (4 wzór), jeśli nie rozumiesz to lekcja 2 z trygonometrii czas 65minuta
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
w przykładzie f, cos^2x zamieniasz z jedynki trygonometrycznej otrzymujesz 1-sin^2x -3sinxcosx + 1 = 0 --->
-sin^2x - 3sinxcosx + 2 = 0 ----> -sin^2x - 3sincosx + 2(sin^2x +cos^2x) = 0 | mozesz tak zrobic bo to równe 1;
-sin^2x - 3sinxcosx + 2sin^2x + 2cos^2x = 0 ---- > sin^2x - 3sinxcosx + 2cos^x = 0 | dzielimy przez cos^2x
tg^2x - 3tg + 2 = 0; podstawiasz t za tg tg nalezy do R , i cosx nie moze byc rowne zero, bo nie mozna dzielic przez 0
i musisz sprawdzic co sie dzieje gdy cosx = 0
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
i jeszcze pytales skad jest 243,5 stopnii, szczerze nie patrzylem dokladnie na to ale ze w tg wiem ze okresowosc to kpi wiec gdy do 63,5 + PI to wychodzi 243,5 bo pi to 180 stopni.
Chyba na wszystko odpowiedziałem, mam nadzieje ze nigdzie się nie pomyliłem lub o czymś zapomniałem bo jeszcze nie robiłem pracy domowej, więc proszę bądź czujny
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
dlaczego w podpunkcie b mamy w odpowiedziach kpi a nie 2kpi? :)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
myśle że z tego wykresu widać ze ten pomaranczowy fragment pojawia się co 6 kratek czyli 6*30stopni to 180 stopni czyli pi
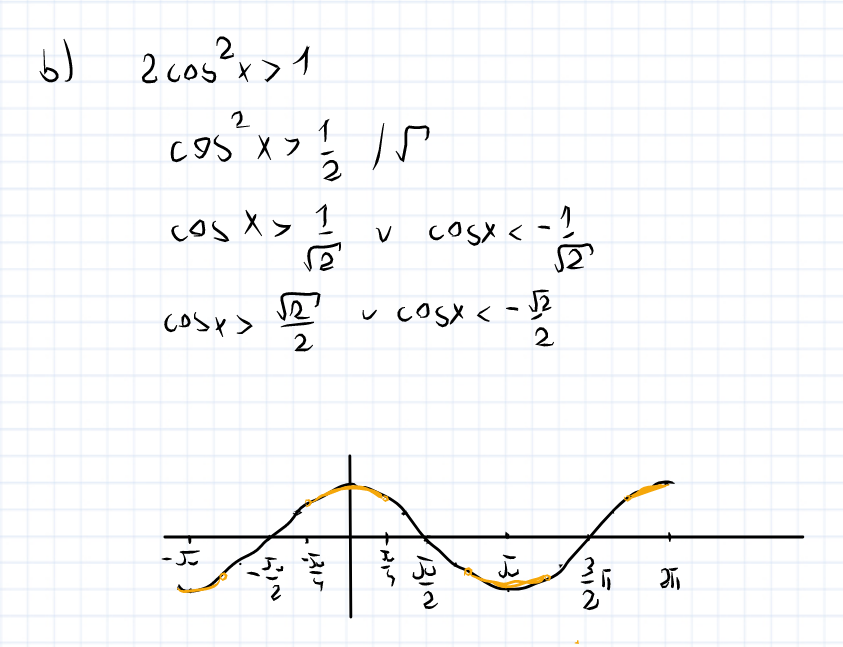
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W przykładzie „f” jak obliczyć ten kąt 243,5 stopni? Wiem skąd się bierze 63,5 stopni, ale nie wiem jak znaleźć kolejny i co do czego dodać.