1c/76 kurs maturalny
Podaj zbiór wartości funkcji: f(x)=sinx*ctgx-cosx*tgx
Czy mógłby mi ktoś wytłumaczyć sens dziedziny w tym przykładzie? Czemu to jest akurat D=R-{kπ/2}?
Niestety nie rozumiem tego.
Zawsze trzeba dawać dziedzinę do takich funkcji? Z czego ona wynika?
dziedzina trygonometria Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jeśli byś nie rozumiał tego co napisałem to mam drugi sposób żebyś to zobaczył. zobacz wykres tg wartości przyjmuje wszędzie prócz wierokrotności pi/2, a wykres ctg to odwrotność tg czyli przyjmuje wartości wszędzie prócz wielokrotności pi, czyli jakby zsumować to i to to nie przyjmuje co kpi/2
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czy możemy zapisać 2 warunki w poniższy sposób?
K(PI) =/= 0
K(PI) : 2 =/= 0
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
nie mozesz drugi warunek źle napisałeś. zsumując te dwa warunku to kpi/2 rózne od zera
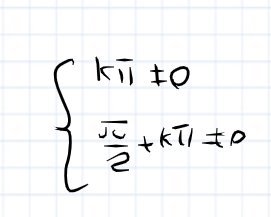
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
gdy rozbijesz ctg na cosx/sinx i tg na sinx/cosx w mianowniku masz sinx który nie moze byc równy zero i cosx tez nie moze byc rowny zero.
x nie moze byc równe kpi bo wtedy sin jest rowny 0 i x nie moze byc rowne pi/2 +kpi bo wtedy cos jest rowny zero
pomiedzy tymi warunkami jest "i" wiec wartość idzie co pi/2 wiec kpi/2, wiec dziedzina to liczby R z wyłączeniem kpi/2