Alex 988 wyśw.
01-11-2020 21:06
7a,b / 110 Kurs maturalny podstawa
Udowodnij,że
A) jeśli XY > 0 to (x+y)*(1/x+1/y)≥4
B) reszta z dzielenia kwadratu liczby podzielnej przez 3 z resztą 2 przez 3 wynosi 1
Proszę o pomoc
matematyka zadanie domowe dowodzenie Dodaj post do ulubionych Poproś o pomoc
Kliknij tutaj, aby dodać nowy komentarz.
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
Grzegorz.p7
04-11-2020 16:31
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Grzegorz.p7
04-11-2020 16:31
jarosinski
04-11-2020 16:31
Ad b) (3k+2)^2 = 9k^2 + 12k +4 = 3 (3k^2+4k+1) + 1 = 3 n +1, gdzie n- liczba całkowita.
Liczba postaci 3n + 1 przy dzieleniu przez 3 daje resztę 1, co należało dowieść.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
julina
02-02-2021 19:44
Mam pytanie co do rozwiązania przykładu a. Jak powstała ta postać?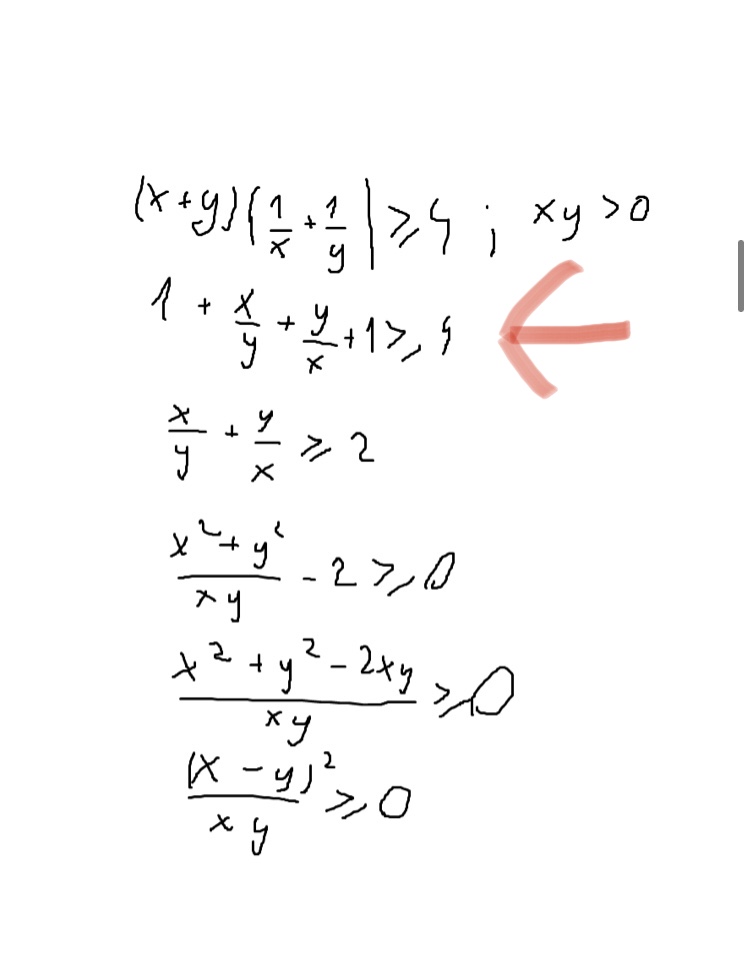 
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Grzegorz.p7
02-02-2021 19:54
@julina
Wymnożyłem nawiasy
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
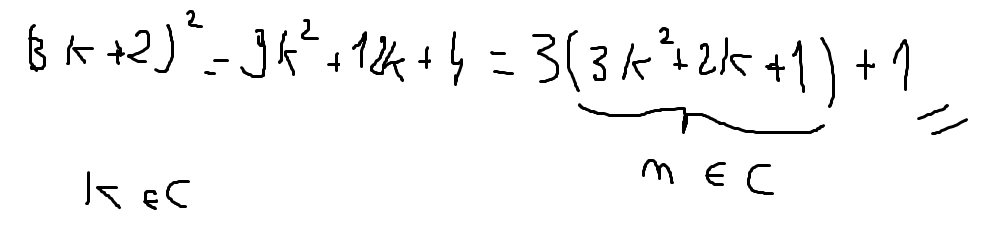
licznik jest wiekszy bądź równy zeru, mianownik wiekszy od zera, wiec udowodnione