KK 658 wyśw. 03-11-2020 12:44

2016.C.10



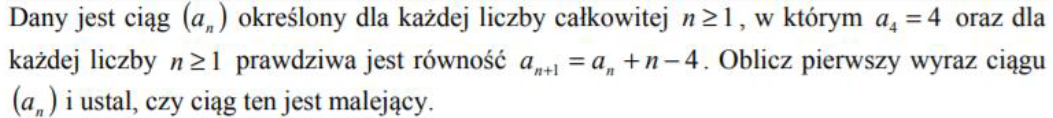
Po wyliczeniu czterech początkowych wyrazów : a1=10, a2=7, a3=5, a4=4 stwierdziliśmy, że ciąg ten nie jest malejący. Na jakiej zasadzie skoro względem kolejnych wyrazów wartość spada?

Matematyka Ciągi Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
tygrysek 04-11-2020 16:31

ponieważ wyszło, że a(n+1)-an=n-4 czyli zalezy to od n a wiemy, że n>=1, czyli podstawiamy sobie, n=1 wtedy a(n+1)-an=n-4 jest ujemne, natomiast gdy n=np.10 jest dodatnie. wiec nie dla całego jest malejący  

jarosinski 04-11-2020 16:31

"Po wyliczeniu czterech początkowych wyrazów : a1=10, a2=7, a3=5, a4=4 stwierdziliśmy, że ciąg ten nie jest malejący."

To zdanie jest nieprawdziwe. Nigdzie podczas wykładu nie stwierdziliśmy monotoniczności funkcji w oparciu o początkowe cztery wyrazy. Stwierdziliśmy ją na podstawie definicji wyliczając a(n+1) - a(n), które wyniosło n- 4. Stąd padł wniosek, że n - 4 nie jest ujemne dla każdego n naturalnego, zatem ciąg nie jest malejący.