4 cz.II/78 Kurs maturalny rozszerzony
Rozwiąż równanie: cosx-2sinx=-1/ pierwiastek z 2.
Mam duże wątpliwości co do odpowiedzi do tego zadania. Czy mógłby ktoś wyjasnić mi na czym polega błąd w moim rozumowaniu?
trygonometria Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
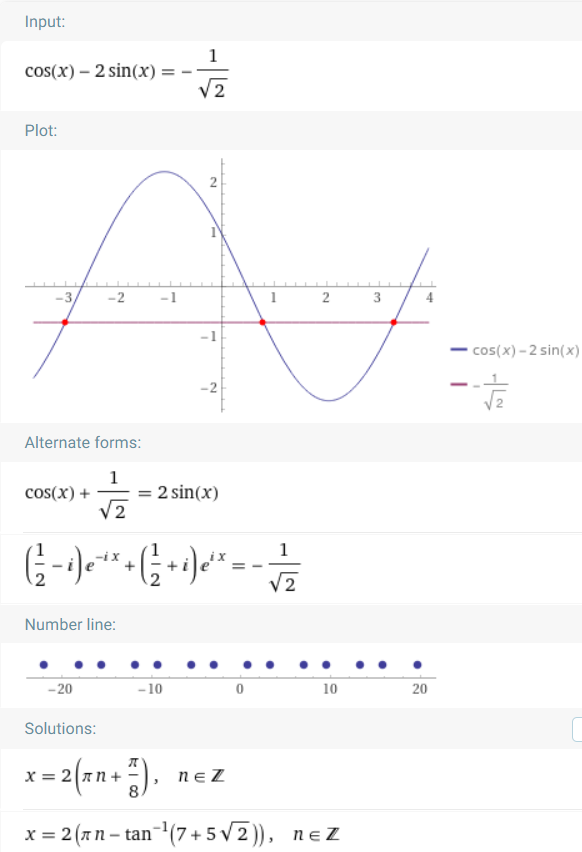
Pan Wolfram potwierdza powyższe rozwiązanie:
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
czy na maturze można zostawić samą odpowiedź arctg(1/7) + kpi? Jeśli nie, to skąd wyczytać jaka to jest wartość w stopniach?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
i jak dokonać tego sprawdzenia czy dane rozwiązanie jest poprawne?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@sara
- można zostawić arctg
- wstawić i sprawdzić :)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czy my podstawiamy za k liczbę 1 i patrzymy czy równość zachodzi, tak parę razy ją inkrementujemy i wyciągamy wniosek, że k jest parzyste?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dalej nie rozumiem jak wykonać sprawdzenie. Prosze o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Pokazałem na przykładzie kąta 8,13:
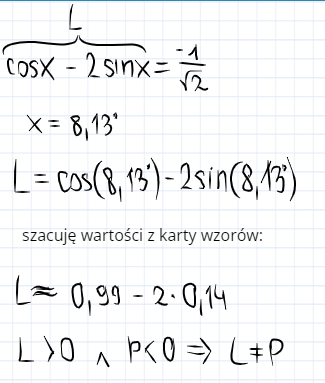
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dziękuje teraz już jasne
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ogólnie są trzy metody rozwiązywania tego typu równań, gdzie sin i cos występują w równaniu w pierwszej potędze:
- wzory na sumy i różnice funkcji trygonometrycznych
- przekształcenie głównego równania tak aby można skorzystać ze wzorów na funkcje trygonometryczne sumy lub różnice kątów
- skorzystanie z jedynki trygonometrycznej (tu trzeba wykonać sprawdzenie bo jedynka tryg. jest równaniem kwadratowym)
W przypadku tego równania działa tylko ostatnia metoda, która jest najogólniejsza (działa zawsze), ale też najtrudniejsza (chociażby ze względu na sprawdzenie).
W kryteriach pojawiła się literówka powodująca, że ogólnie jest błąd, który wyłapałeś. Oto poprawne rozwiązanie: