6a,c/79 Kurs maturalny rozszerzony
Dla jakich wartości parametru p ciąg o wyrazie ogólnym an=pierw(4n^2 + 3n +5) - (pn+1)
a) ma granicę niewłaściwą -(nieskończoność)
b) ma granicę właściwą (liczbę) - oblicz tę granicę
c) ma granicę niewłaściwą +(nieskończoność)
Jak rozpisać podpunkty a i c?
granice Dodaj post do ulubionych Poproś o pomoc
- 11
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1. jak policzyć podpunkt b) ??
2. czemu w odpowiedziach w książce dla c) jest p e (-niesk;2), skoro ,wg tego co Pan napisał powyżej, jest (-niesk;-2) U (-2;2) ???
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@Nazwa:
"skoro ,wg tego co Pan napisał powyżej, jest (-niesk;-2) U (-2;2) ???" -> przeczytaj proszę dokładnie całość. Dla -2 oraz 2 trzeba zrobić osobne obliczenia o czym napisałem: "Ale jak się podstawi te dwie wartości, to się okazuje, że dla p = -2 jest jednak rozbieżna"
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ad b) granica ma szansę być zbieżna tylko wtedy, gdy p = 2 lub p = -2. Należy podstawić te wartości i obliczyć osobno granice dla tych wartości. Dla p =2 będzie ona zbieżna, dla p =-2 rozbieżna
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czy wyciągając n^2 z pierwiastka, nie powinien być |n| ?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
dla p=-2 wychodzi [7/0]. w jaki sposób mam ustalić znak zera?? pamiętam jak ustalaliśmy na lekcji, ale tam była granica w punkcie
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@hm: nie, ponieważ to jest ciąg (n jest naturalny), zatem |n| = n
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@Nazwa: 0 jest na plusie, ponieważ n jest liczbą dodatnią (jako naturalna), zatem pod pierwiastkiem mamy tak jakby sqrt( 4,0000...), czyli dążymy do 4 z prawej strony i ona się spierwiastkuje jako 2 do której dążymy z prawej strony (2,000...). Minus byłby gdyby pod pierwiastkiem było tak jakby 3,999...
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
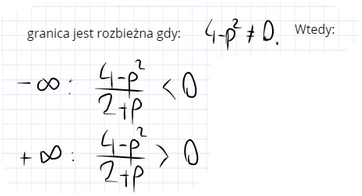

Należy doprowadzić granicę do możliwie najprostszej postaci (rys.) i z niej wyciągać wnioski. Granica ma szansę być zbieżna tylko wtedy, gdy p = 2 lub p =-2. Ale jak się podstawi te dwie wartości, to się okazuje, że dla p = -2 jest jednak rozbieżna. W liczniku przy najwyższej potędze "n" stoi wyrażenie 4-p^2, a w mianowniku przy najwyższej potędze 2+ p (dwójka wzięła się z pierwiastka 4). Skoro stopień licznika dla p różnych od -2 oraz 2 jest wyższy niż mianownika to granicą będzie nieskończoność. O znaku tej granicy (plus lub minus) będzie świadczył iloraz 4-p^2 / 2+p.