5hj/79 Kurs maturalny rozszerzony
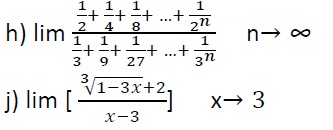
Czy mógłby mi ktoś wytłumaczyć przykład h i j z zadania 5? Kompletnie nie wiem jak się za nie wziąć:(
granice Dodaj post do ulubionych Poproś o pomoc
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W pkt h korzystamy ze wzoru na sumę szeregu geom. Dobrze rozumiem? Nie na sumę poczatkowych wyrazow ciagu geom. Bo trochę dziwnie to ujeles
Plus czy moglbys wytlumaczyc gdzie jest ten wzor na roznice szescianow jak tam jest w liczniku a+b, a nie a-b. Bo ja za bardzo nie łapię
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ten wzór, który używamy aby wyliczyć sumę ciągu geom. nazywa się suma n początkowych wyrazów ciągu geom., dlatego to tak ujęłam. Te ciągi są skończone, nie są szeregami, ponieważ szereg to nieskończonay ciąg geometryczny.
Natomiast w podpunkcie j) popełniłam błąd ze znakami, już poprawiam w poprzednim komentarzu
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Okej Anonim dzięki za wyjaśnienie. Pomogłabyś mi moze z jednym jescze bo
widze ze rozumiesz. 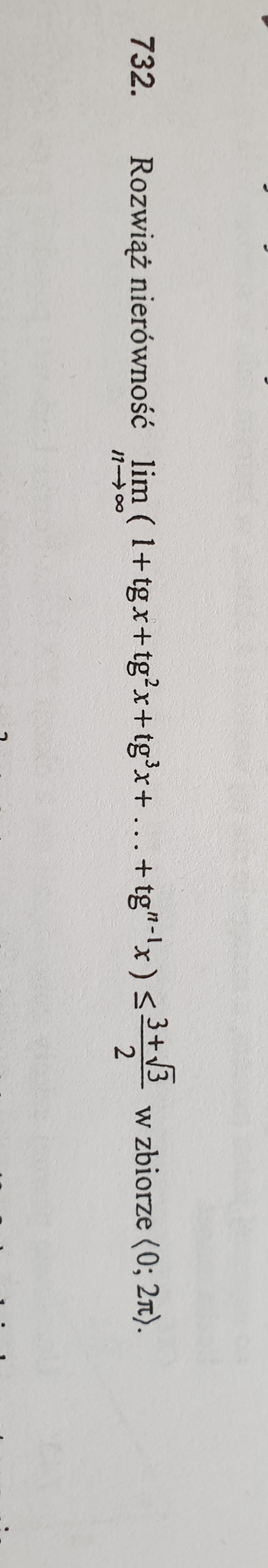 tu w tym to po lewo masz sumę n poczatkowych wyrazow ciagu geo? Bo w internecie ludzie robia ze wzoru na sume szeregu i juz sama nie wiem.
tu w tym to po lewo masz sumę n poczatkowych wyrazow ciagu geo? Bo w internecie ludzie robia ze wzoru na sume szeregu i juz sama nie wiem.
Pozdrawiam
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak, lewą stronę rozwiazujesz ze wzoru na sumę początkowych wyrazów ciągu, a1=1 i q=tgx. Następnie wyznaczasz granicę i rozwiazujesz nierówność
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dzięki Anonim!
Mam prośbę, wyslalabys swoje rozwiazanie tego zadania? Bo z tego wzoru to mi wychozi nieskonczonosc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Już to rozwiążę, a masz napisane jaki jest wynik?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A czemu założyłaś ze |tgx|<1?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Oj, odruchowo.
Wynik się zgadza, na pewno musi być tgx różny od 1, bo jest w mianowniku. Muszę to przeanalizować
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nwm wydaje mi sie ze trzrba tak zalozyc bo inaczej byla by nierownosc sprzeczna no ale nie wiem. Jak do czegos dojdziesz to daj znac proszę
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wychodzi na to, że trzeba to rozwiązać ze wzoru na szereg, ale jest to przecież skończony ciąg geometryczny.
Napisałam do Pana Łukasza
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W przykładzie h) występuję suma n wyrazów ciągu geometrycznego. Ale granica tej sumy ciągu w nieskończoności to szereg! Dokładnie w taki sposób wyprowadziłem wzór na szereg na lekcji :) Dlatego można zrobić to dwojako
1) policzyć tą granicę (i wyjdzie Ci szereg)
2) od razu zastosować wzór na szereg do licznika i mianownika
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
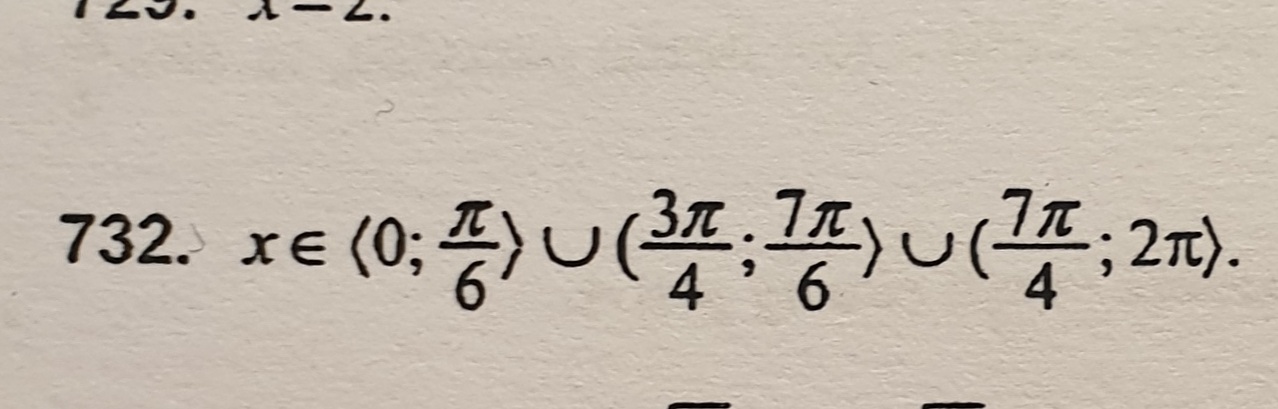 Dziękuję
Dziękuję 
W podpunkcie h) zarówno w liczniku jak i mianowniku występują ciągi geometryczne. Musisz skorzystać ze wzoru na sumę początkowych wyrazów ciągu geom. W liczniku a1=1/2 i q=1/2, w mianowniku a1=1/3 i q=1/3. Korzystając z tych danych zapisujesz wzory na sumy i obliczasz granicę.
W podpunkcie j) po podstawieniu 3 za x pojawia się symbol nieoznaczony. Należy tak rozpisać ten ułamek, aby "pozbyć się" z mianownika x-3. Zauważ, że w liczniku występuje część wzoru na sumę sześcianów: a^3 + b^3 =(a+b)(a^2-ab+b^2). To co jest w liczniku to jest (a+b), więc teraz musisz "dopełnić" ten wzór wymnażając przez tzw. sztuczną jedynkę dalszą część wzoru, czyli przez (a^2-ab+b^2)/(a^2-ab+b^2). Następnie zwijasz wzór w liczniku i zauważasz, że pojawia się w nim x-3 (po wyciągnięciu -3 przed nawias), które skróci się z x-3 w mianowniku. Teraz tylko podstawiasz 3 pod x i wychodzi granica.
W razie czego pisz, podeślę zdjęcia z moim rozwiązaniem ;)