medi 922 wyśw.
17-11-2020 22:05
5a/79 Kurs maturalny rozszerzony
5/79
oblicz granicę:
a) lim (1 + 0,5 + 0,5^2 + 0,5^3 +...+0,5^n) n -> nieskończoność
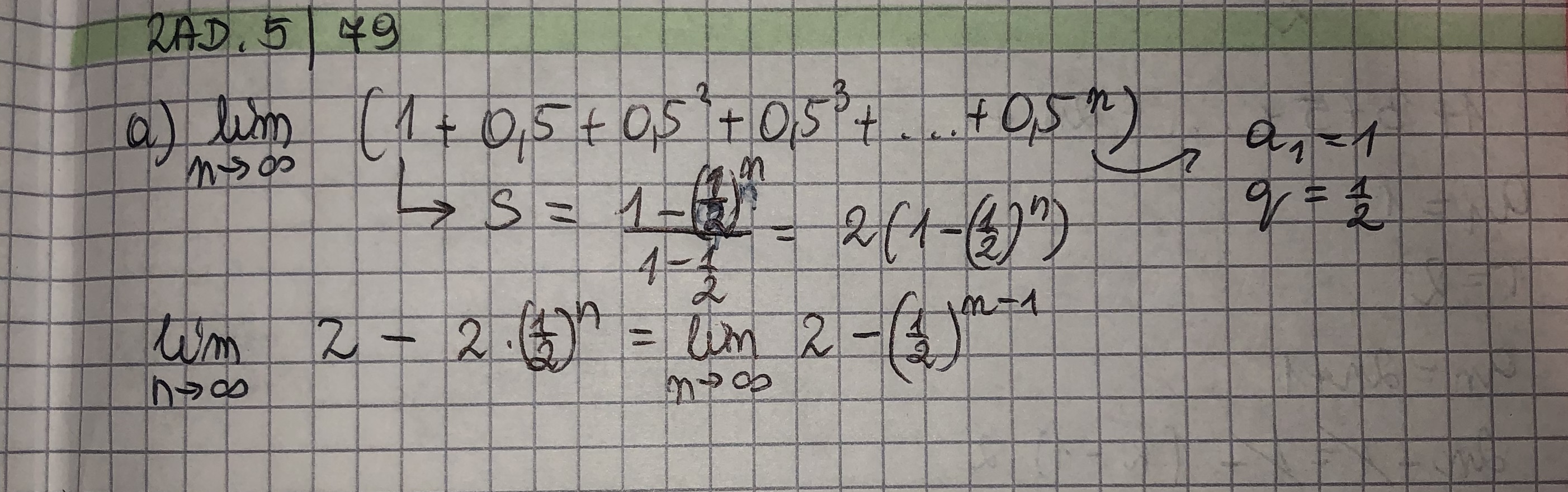Hej, czy ktoś może mi pomóc z dokończeniem obliczania tej granicy lub wskazać błąd jaki już popełniłem?
Doszedłem do czegoś takiego:
matematyka granice Dodaj post do ulubionych Poproś o pomoc
Kliknij tutaj, aby dodać nowy komentarz.
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
Grzegorz.p7
17-11-2020 22:12
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Lutwik
17-11-2020 22:17
Wyszło Ci 2-(1/2)^n-1 Z tego wynika, że granicą liczby 2 jest liczba 2, natomiast drugiego składnika dla n dążącego do nieskończoności jest 0. Wynika to z tego, że podstawa potęgi jest mniejsza od 1 a wykładnik dąży do nieskończoności, więc posługując się definicją 1/2^n-1 dąży do 0. Granica więc jest równa 2-0=2
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Użyłeś złego wzoru, powinieneś użyć wzoru na Sume wyrazów nieskończonego ciągu geom.
bo:
przy |q| < 1