2020.8/37
Liczby dodatnie a i b spełniają równość a^2 + 2a = 4b^2 + 4b
Zrobiłem to zadanie 2 sposobami, ale zależy mi zrobić je metoda funkcji kwadratowej ale dochodzę do pewnego momentu i nie wiem co zrobić.
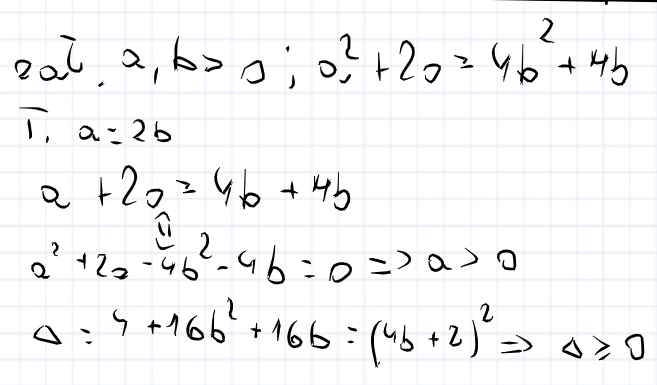
udowodniłem tylko że a +2a - 4b - 4b >= 0, a nie, że a = 2b
udowodnij funkcja kwadratowa Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
nie do końca dalej rozumiem, mógłbyś bardziej jeszcze wytłumaczyć?
czemu W = 0, gdy delta >= 0
potem odrzucamy b1 i kolejne wnioski, których nie rozumiem
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W=0 w miejscach zerowych tzw. Wiec aby te miejsca zerowe byly to delta musi byc =/> 0 bo jak delta jest <0 to wtedy nie ma miejsc Erowych wiec to by bylo sprzeczne.
Wiec jak juz do tego doszlismy to tą delte wyliczamy i wyszlo nam te (4b+2)2 i yo musi byc >/=0 no i sobie sprawdzamy ze ta delta jest =0 dla b=-1/2 a z zalozenia wiemy ze b>0 wiec b=-1/2 nie jest w naszej dziedzinie. Z tego wzgledu dla wszystkich b>0 (bo takie mamy w zalozeniu) ta delta jest >0. Skoro to wiemy to delta >0 ma tzw 2 miejsca zerowe. Wyliczamy je a2 i a3 na obrazku masz wyliczone. Jedno z nich mie nalezy do dziedziny a bo a>0 a drugie a=2b nalezy do dziedziny bo 2b> 0 i a>0.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
dziękuje za pomoc, już rozumiem
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ja zrobiłam w ten sposób, więc może pomogę. Jak ktoś też zrobił tą metodą to może sprawdzić, żeby nie było niechcianych nieprawidłowości :)
Pozdrawiam :)