1b/80 Kurs maturalny rozszerzenie
udowodnij, że dla dowolnych liczb x, y zachodzi nierówność 3x^2 + 4x^2 - 8xy + 2x^2^y^2 + 3 > 0
Mógłby mi ktoś sprawdzić czy dobrze zrobiłem to zadanie sposobem funkcji kwadratowej? bo w odpowiedziach jest inny przedstawiony inny sposób
Jako, że dużo komentarzy pod postem postanowiłem edytować, żeby każdy kto chce mógł znaleźć z tego posta co chce.
błąd zrobiłem w linijce 8, gdy dzieliłem przez liczbę ujemną(nie można tak przez to zmieniłem współczynik a), przez co moje wnioski są błędne, gdybym nie podzielił przez liczbe ujemną mam wspol. a delty < 0 idelte delty < 0 co daje nam pierwszą delte < 0 czyli
a > 0
delta < 0 zatem: W > 0
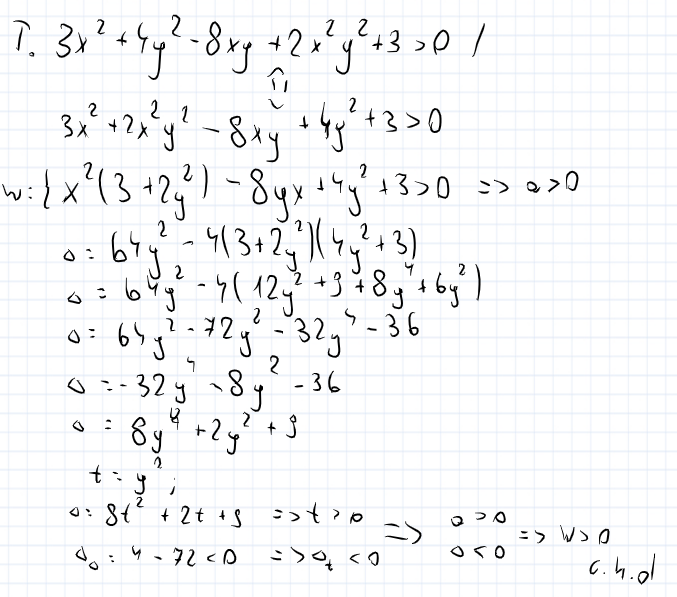
udowodnij funkcja kwadratowa Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie wiem własnie jak sobie to wyobrazić, dlatego pytam
gdy t > 0 i delta delty < 0 to wykres mamy nad osią ox czyli brak miejsc zerowych, czyli to nam mówi, że pierwsza delta jest ujemna i a > 0 bo to na początku zadania wykazałem?
Dobrze sobie to przedstawiam czy gdzieś błądzę.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jak masz delte = -32y4-8y2-36 to po wyliczeniu delty z tego (po podstawieniu t)ta delta jest ujemna a a=-32 wiec ten wykres znajduje sie pod osia ox. Czyli funkcja -32t2-8t-36 przyjmuje wartosci ujemne (bo wykres pod osia ox) wiec ta funkcja=delta wiec delta tej 1 funkcji (ktora masz na początku) jest ujemna. Skoro delta jest ujemna a a jest >0 to W jest nad osia x czyli jest dodatnie.
T=/>0 bo y2 moze byc 0.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
dziękuje bardzo, czyli ta druga delta musi być zawsze ujemna i a < 0, i wtedy się zgadza sie nasza teza Wyrażenie > 0, a gdyby było że druga delta < 0 i a > 0 to juz nasza teza sie nie zgadza, tak?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Gdyby 2 delta <0 i a>0 to wykres masz nad osia czyli -32t2-8t-36 przyjmuje wartosci dodatnie. A -32t2-8t-36=1 delta. Wiec 1 delta >0 i a>0 wiec W nie jest dodatnie (ma dwa miejsca zerowe itp.) Wiec to by bylo sprzeczne bo W musi byc >0 dla kazdego x i y.
Jeszcze jedno : mozesz od razu gdy wysza ci delta = -32y4-8y2-36 to od razu mozesz stwierfzic ze delta jest ujemna bo y4>\=0 i y2>\=0 i wtedy roznica liczb nieijemnych i liczby ujemnej zawsE daje liczbe ujemna. I juz masz dowod na to nie yrzeba liczyc nast delty i jest krocej. To tak na marginesie
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie można wykonać takiej operacji dzielenia delty przez liczbę ujemną. Z delty ujemnej zrobiłeś tym sposobem dodatnią
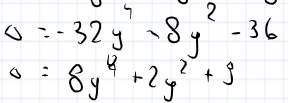
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dziękuje wam bardzo, wszystko już jest dla mnie jasne
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
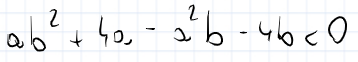
w takim wypadku pierwsze a < 0 i delta < 0,
a drugie a > 0 i delta > 0, tak?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie chce robić kolejnego postu z pytaniem o dowodzenie w funkcji kwadratowej, dlatego zapytam tutaj, nie udowodniłem tezy, bo wyszła mi delta równa zero zatem znak w Tezie musiałby być <= zamiast < ?, więc muszę użyć innego sposobu, tak?
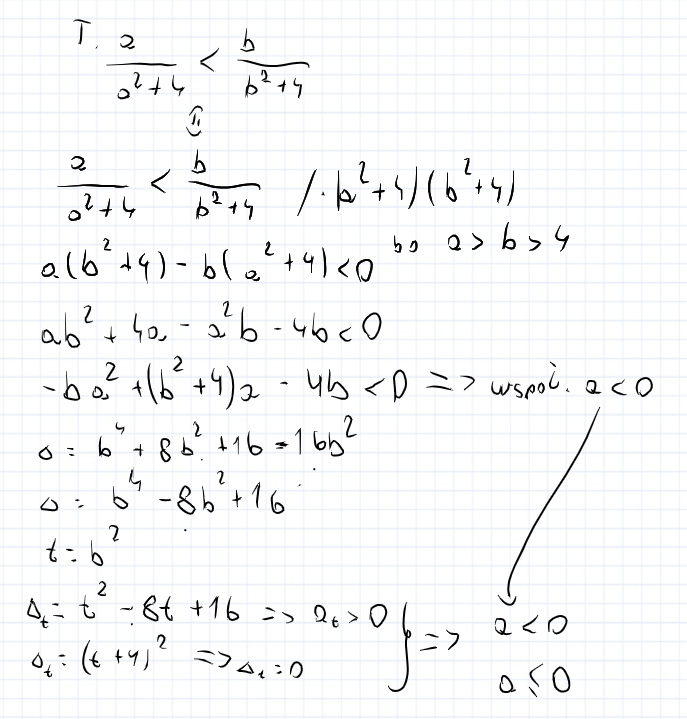
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1 sposobem zrobiłem czyli z założenia bardzo prosto, a z funkcji kwadratowej jeszcze będe próbował potem jeszcze tu prześle czy sie udało w końcu jakoś. Próbuje tą funkcje kwadratową dobrze ogarnąć, żeby jak coś mieć ten plan B na maturze
Widze ze teraz edytowałes, czyli tak jak myślałem tamto zdj co wysłałem wcześniej jest speczne?i musze innaczej probowac?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wiesz co ja tez staralam sie robicwiekszosc gl z funkcji miedzy innymi ale nie zawsze moim zdanie sie da bo wyslalam wyzej zfj czemu moim zdaniem tu to nie wyjdzie a jak przed chwila spr ze jak wezmiemy zrobimy funkcje b2a-b(a2+4).... to od buta nie wyjdzie bo amusi byc <0 zeby W<0 a tu juz masz a>0 bo z zal. wiesz ze a>2 tak mi sie wydaje. Ale moze spytaj Pana Łukasza, on ci pomoze
Tak edytowalam, bo spojrzalam na to jeszcze raz imi nie pasowalo po prostu (cala prace dom robilam po nocach)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
będę jeszcze próbował rozwiązać za pomocą funkcji kwadratowej, różnymi sposobami jak wyjdzie to prześle tutaj rozwiązanie, a tobie Wielkie dzięki za pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Bylo by super , to sobie zerkne, tez posiedze jeszcze nad tym dzisiaj. Powodzenia!
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
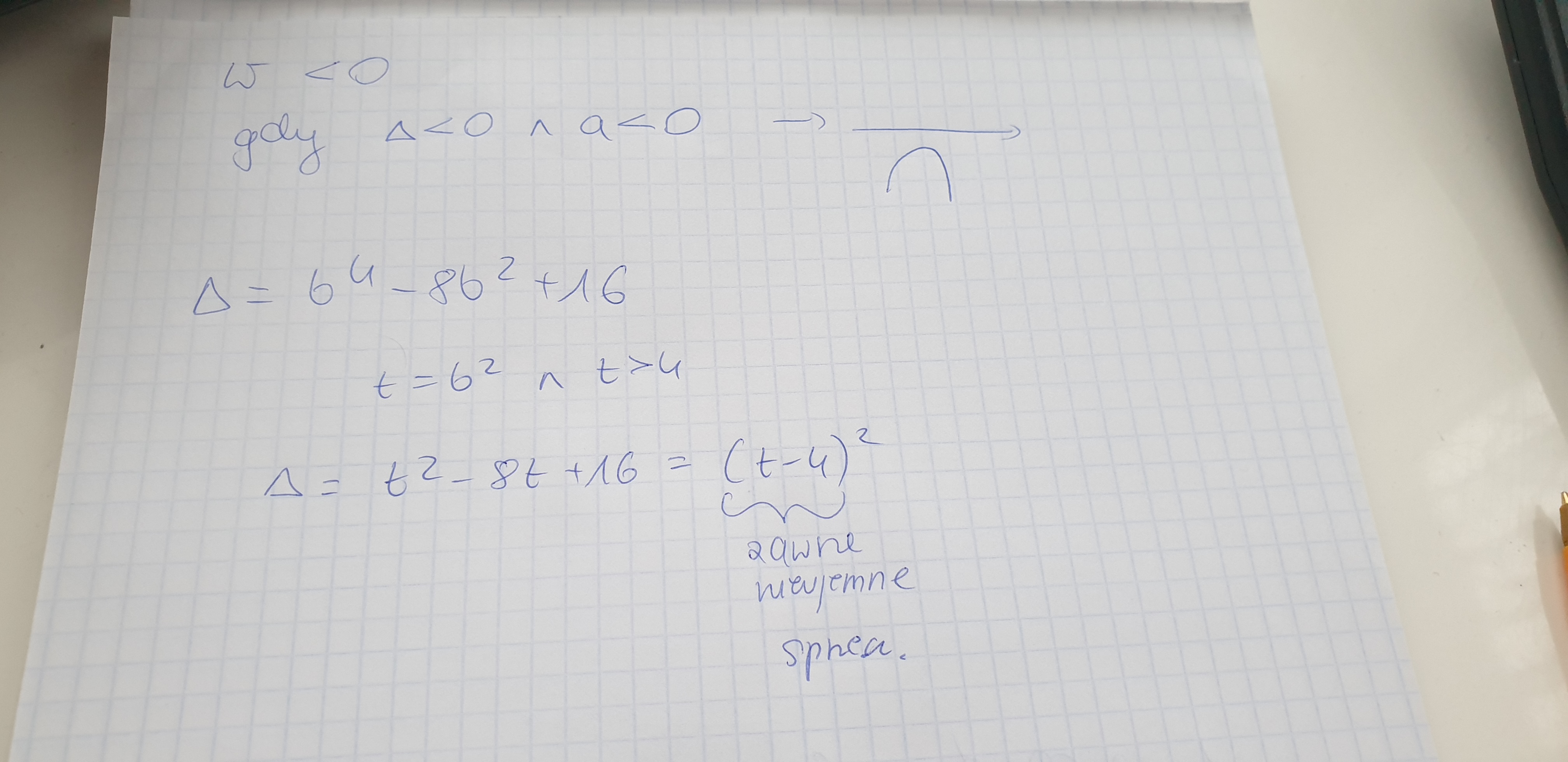
Wydaje mi sie ze dobrze. Ja jeszcze dokladniej napisalam czemu a>0 na wszelki wypadek :,D