3 /80 Kurs maturalny rozszerzony
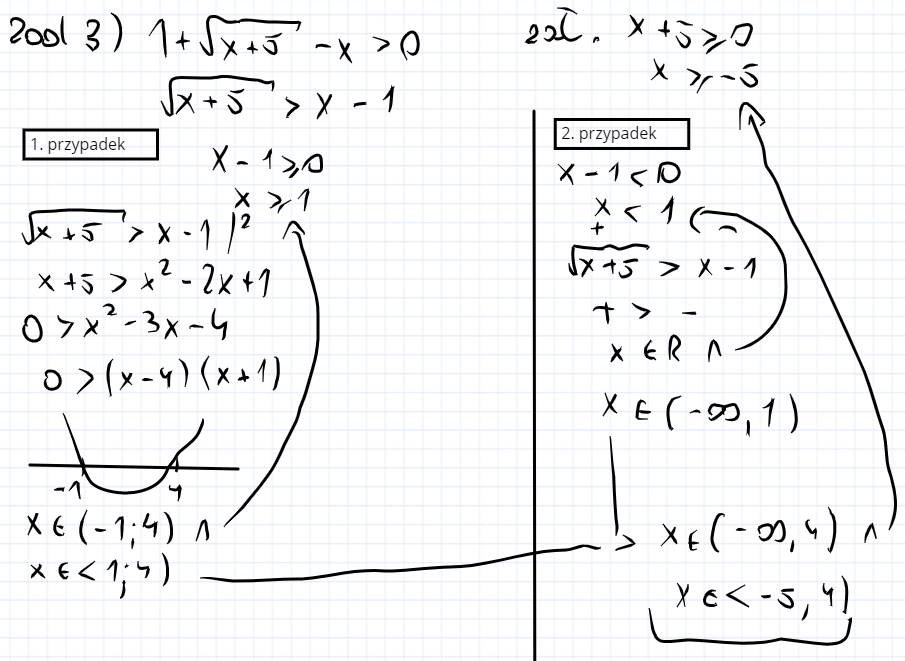
Rozwiąż nierówność 1+pier(x+5) -x > 0
Czy mógłby ktoś rozpisać? Kryteria w odpowiedziach nie za bardzo mi pomogły
Matematyka Dodaj post do ulubionych Poproś o pomoc
I) Ustalasz globalne założenie czyli to co pod pierwiastkiem musi być większe bądź równe zero
II) przerzucasz zmienną i liczbę na druga stronę, a pierwiastek zostawiasz po lewej
III) rozbijasz zadanie na dwa przypadki I gdy to co mamy po prawej jest większe bądź równe zero i drugi przypadek kiedy to co po prawej stronie jest mniejsze od zera.
IV) w 1 przypadku możesz podnieść do kwadratu bo obie strony są dodatnie i uwzględniając twoje założenie ustalasz do jakiego zbioru nalezy x
V) w przypadku drugim masz, że to co po prawej stronie jest ujemne, a pierwiastek jest zawsze dodatni
wiec masz wyrażenie + > -, więc rozwiązaniem jest R, teraz ustalasz rozwiązania dodajać twoje założenie,
VI) Rozbiłeś wyrazenie od -oo do 1 i od 1 do +oo, więc musisz je zsumować oraz uwzględnić globalne założenie.
Warto dodać ze drugi przypadek zawsze jest R lub zbiorem pustym dzieje się tak
ponieważ drugą opcją mogłoby byc ze znak pomiedzy wyrażeniami jest w drugą strone wtedy to co pod pierwiastkiem jest dodatnie po lewej stronie dalej liczbe ujemna, czyli otrzymujemy + < 0 co jest oczywiscie nie prawda
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych