xxx 731 wyśw. 20-11-2020 16:24

2012.C.6

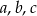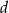Udowodnij, że dla dowolnych liczb dodatnich $a,b,c$ i $d$ prawdziwa jest nierówność

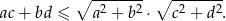
∘ ------- ∘ ------- ac + bd ≤ a2 + b2 ⋅ c2 + d2.

można zrobić to zadanie na podstawie nierówności między średnimi? zrobiłam już z dopełniania do kwadratu i zastanawiam się nad drugim sposobem :)

matematyka matura Dodaj post do ulubionych Poproś o pomoc

Kliknij tutaj, aby dodać nowy komentarz.

Zaloguj się lub zarejestruj, by móc dodawać komentarze.

jarosinski 21-11-2020 23:06

Po krótkiej analizie nie znalazłem opcji udowodnienia tej nierówności korzystając z nierówności pomiędzy średnimi. Dlatego też na lekcji podkreślałem, że około 90% zadań w których zmienne są dodanie dotyczy nierówności pomiędzy średnimi. Równie dobrze może być zadanie w którym zmienne są dodatnie, a dowód należy przeprowadzić korzystając bezpośrednio z założenia (tak jak tutaj).

0
Zaloguj się lub zarejestruj, by móc oceniać komentarze.
Dodaj do ulubionych

jarosinski 21-11-2020 23:06

Nie mniej jednak nierówności pomiędzy średnimi nieraz mnie zaskakiwały i nie zamykam ostatecznie tego tematu :)

0
Zaloguj się lub zarejestruj, by móc oceniać komentarze.
Dodaj do ulubionych

JA 21-11-2020 23:14

https://www.overleaf.com/read/ktqhgdfsvbqb

to jest link do pliku w Latexu, z rozwiązaniem, link jest bezpieczny, oczywiście jak zaznaczyłem w rozwiązaniu mogę się mylić

0
Zaloguj się lub zarejestruj, by móc oceniać komentarze.
Dodaj do ulubionych

iza 23-11-2020 22:26

Czy można byłoby prosic o jakies wskazówki, albo rozwiązanie tego zadania tym sposobem którym zrobiłaś?

0
Zaloguj się lub zarejestruj, by móc oceniać komentarze.
Dodaj do ulubionych