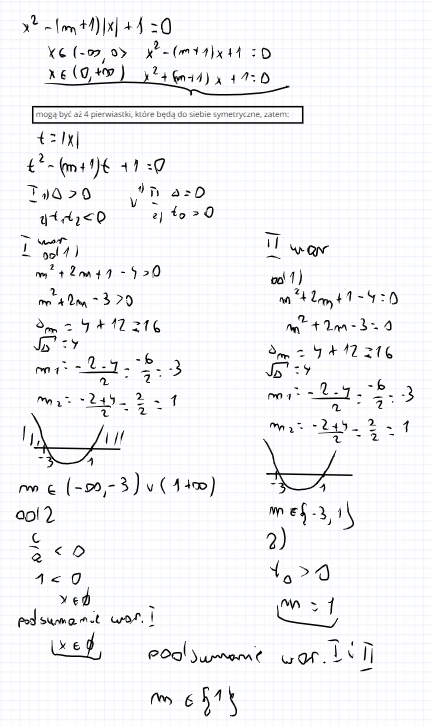Zadanie 2 zadanie domowe nr 10 cz2/ 80

jest to ss, z 2 lekcji z wielomianów, na poprzednim zdjęciu ci pokazałem, że mamy możliwośc uzyskania 4 rozwiązań, ale my chcemy tylko 2, od razu wyrzucamy możliwość funkcji liniowej bo u nas a jest różne od zera, a więc

1 warunek, gdy delta jest większa od zera otrzymujemy t1 i t2 czyli 4 rozwiązania bo gdy podstawimy t = |x| otrzymujemy dwa rozw dla każdego t, ale t1*t2 < 0 gwarantuje nam, że jedno jest dodatnie a drugie ujemne czyli np mając -5 = |x|, wiemy, z własności wartości bezwględnej że to równanie jest sprzeczne, wiec zostaje nam jedno t > 0 czyli z niego dostajemy dwa x,

2 warunek delta równa 0 czyli mamy jedno t, z którego mamy dwa x, ale żeby dostać na pewno dwa x, to t musi byc też większe od 0, bo jakby t było równe -3 to znów mamy -3 = |x| czyli sprzeczne, ale już np 5 = |x| to mamy x = -5 lub x = 5

Dziękuję bardzo, już wszystko rozumiem :)

nie rozumiem skąd wzieło się m^2+2m+1-4>0