Dowodzenie podzielności poprzez rozbijanie na podzbiory
Przykładowe zadania: 2018.8 i 2016.S.7, które były robione na lekcji


Czy mógłby ktoś wytłumaczyć w jaki sposób dowodzi się podzielności rozbijając zbiór liczb na podzbiory? Chciałbym żeby to pytanie było bardziej precyzyjne, ale nie rozumiem samej mechaniki działania tej metody. Największy problem sprawia mi zrozumienie zadania 2018.8 ze strony 37, które było wykonywane na lekcji właśnie tym sposobem. Nie wiem jak w głowie zwinąć kilka przypadków w mniejszą ilość i jak się to odbywa. Z góry dziękuje za pomoc.
Dowodzenie podzielności Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Na nowym nagraniu które jest już na stronie starałem się to tłumaczyć jeszcze dokładniej. Należy dołożyć wszelkich starań żeby to zrozumieć ponieważ jest to podstawowa metoda dowodzenia podzielności. Rozbijamy na podzbiory z dwóch powodów:
1) ponieważ zawsze możemy tak zrobić
2) ponieważ umożliwi nam to dowodzenie (poprzez pojawienie się odpowiednich wyrażeń).
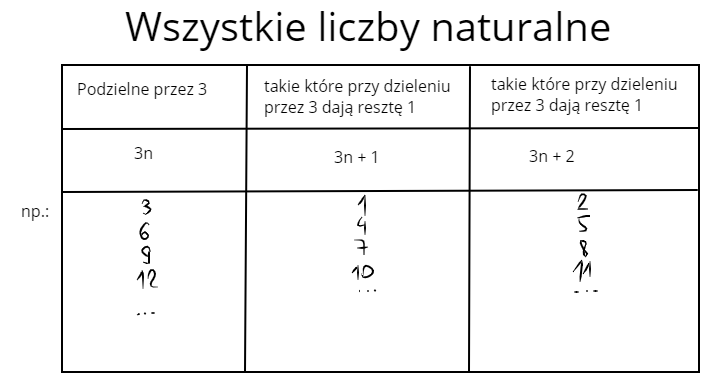
I tak jeśli mamy udowodnić np. podzielność przez 3 to dzielimy zbiór liczb całkowitych (lub zbiór liczb naturalnych w zależności od zadania) na 3 podzbiory. Jeśli dowodzilibyśmy podzielność przez 5 to dzielilibyśmy na 5 podzbiorów itd. W przypadku np. dowodzenia podzielności przez 3, dzieląc na podzbiory pojawiają się odpowiednie wyrażenia typu 3n, 3n + 1 oraz 3n + 2 które bardzo ułatwiają przeprowadzenie dowodu.
- 3
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
gdzie na stronie bede mogl znalezc owe nagranie? @jarosinski
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
moje kursy --> Zawartość
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
mechanizm:
Masz z zadania km(k-m)(k+m)
tak na prawdę nic o tym nie wiesz bo nie są one w kolejności po sobie
Ty chcesz udowodnić ze dzieli się ona przez 6, liczba dzieli się przez 6 wtedy gdy liczba dzieli sie przez 2 i przez 3, więc to musisz udowodnić.
Więc rozbijasz to na kilka przypadków, osobno udowadniasz że dzieli ją 2 i 3. Musisz rozpatrzyc wszystkie przypadki
to przypadki dla 2
1) gdy obie liczby dzielą 2 ----> 2,4,6,8 itd
2) jedna z nich dzieli a druga nie ----> 2,3 lub 3,2; 4,3 lub 3,4 itd
3) obie jej nie dzielą ----> 1,3,5,7,9 itd
wszystkie możliwości Czyli rozpatrujesz 3 przypadki które, dają ci zbiór liczb Rzeczywistych, więc rozpatrując je sprawdzasz wszystkie liczby
1 przypadek k = 2a i m = 2b (a,b to liczby Całkowite to z zał.) czyli ten warunek mówi ci ze k i m dzielą się przez 2, podstawiajac pod wzó otrzymujesz ze jest podzielna przez dwa, bo 2 da sie wyciągnąc przed nawias
2 przypadek (k = 2a + 1 i m = 2b) lub (k = 2a i m = 2b+1) czemu tutaj rozpatrujemy dwa przypadki naraz ponieważ są to liczby do siebie symetryczne, więc wyjdzie ten sam wniosek, i ten przypadek mówi ci że jedna liczba jest podzielna przez dwa, a druga nie jest bo mamy reszte 2, że wychodzi ten sam wniosek to na końcu zamieściłem ss.
3 przypadek k = 2a + 1 i m = 2b + 1, z tego przypadku znów podstawiając wychodzi ze liczba jest podzielna przez 2,
Z tych przypadków jesteśmy juz pewni ze nasza liczba jest podzielna przez 2 bo rozpatrzyliśmy wszystkie przypadki jakie są możliwe, i teraz trzeba udowodnić że ta liczba też jest podzielna przez 3 w analogiczny sposób
Napisz mi proszę czy zrozumiałeś