1k/80 - rozwiązanie przy użyciu funkcji kwadratowej
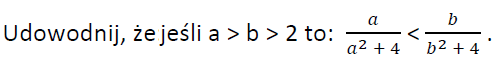
Po przemnożeniu na krzyż próbowałem potraktować całość jako funkcję kwadratową, gdzie a jest argumentem, a b parametrem, a całość ma być większa od zera.
a2 *b - a(b2+ 4) + 4b > 0
Doszedłem do wniosku, że jest to spełnione dla:
1) Delty < 0, b > 0 2) Delty >= 0 i a1, a2 <= 2
Pierwszy warunek nie jest spełniany nigdy, natomiast w drugim wychodzą same głupoty. Czy ktoś umiałby przedstawić pełne rozwiązanie tą metodą? Spędziłem nad nim cały wieczór, ale chyba zbyt się pogubiłem i zafiksowałem w obliczeniach...
Dowodzenie funkcja kwadratowa nierówność Dodaj post do ulubionych Poproś o pomoc
Warunki są identyczne jak twoje, natomiast napisałeś, że w drugim wychodzą same głupoty. Mi wyszło w miarę sensownie. Napisz mi co myślisz o tym rozwiązaniu bo wydaje się być poprawnym.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czyli w II również zakładamy, że a > b > 2? Wtedy wychodzi sprzeczność z założeniami że a1 + a2 <= 4. A jeśli nie zakładamy tego, że a > b > 2 to nie możemy bezkarnie pomnożyć przez b, co psuje całe rozwiązanie
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
rozwiązując nierówności i szkicując wykres. zaznaczasz miejsca zerowe nawet jak są poza dziedziną. Zaznacz o który fragment ci dokładnie chodzi z tą sprzecznością.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wychodzi nam, że dla b = 0 jest spełniony warunek, że a1 + a2 <= 4, a dla reszty a1+a2 > 4, czyli jest sprzeczne z tym co chcemy udowodnić.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Przecież dla b=0 jest sprzeczny ten układ równań. 
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Faktycznie, zapomniałem o tym. Dziękuję bardzo.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jednak mam jeszcze jedno pytanie. Czy w tym miejscu nie powinien być odwrotny znak?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
I teraz powiem ci, że mam wątpliwości czy da się zrobić to zadanie tą metodą...
Nie mam pomysłu szczerze, bo faktycznie uwzględniając te założenia to powinien ten iloczyn być dodatni, ale wtedy gdy użyjemy wzorów viete'a to nie damy rady tego udowodnić ( przynajmniej tak mi się wydaje). Poprosiłbym jednak w tym przypadku Pana Jarosińskiego o pomoc, bo wyczerpały mi się pomysły.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Z metody funkcji kwadratowej korzysta się wtedy gdy trzeba udowodnić nierówność dla każdego x należącego do R. W przeciwnym przypadku mogą wychodzić takie klocki.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
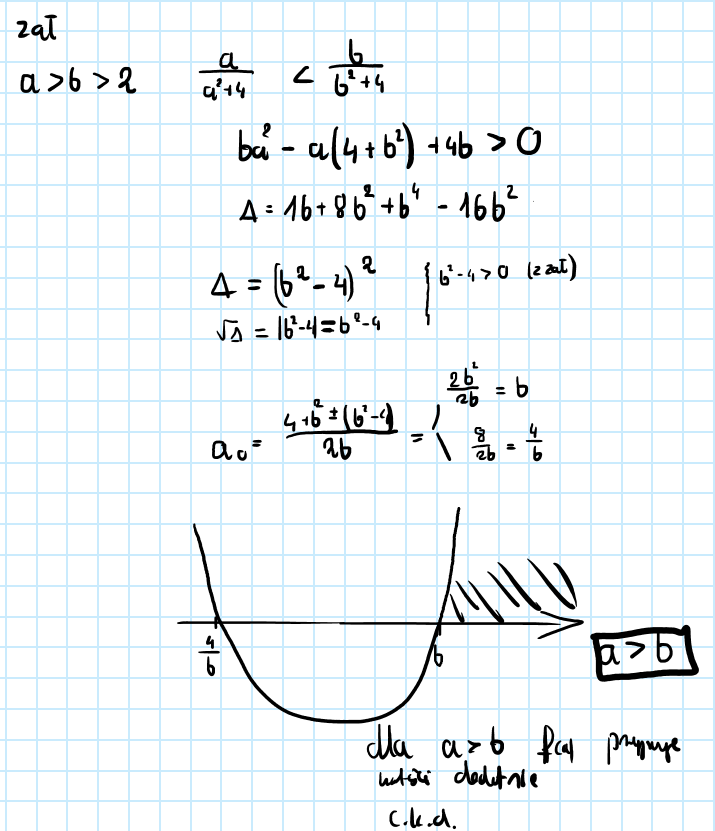
A czy takie rozwiazanie tego z wykorzystaniem metody funkcji kwadratowej jest w porzadku? Delta wychodzi pierwiastkowalna, więc możemy obliczyć miejsca zerowe co w połaczeniu z założeniem pozwa wykazać tezę
Jeśli można tak to zrobić, to czy powinienem jeszcze coś dodatkowo opisać, czy jest okej?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych