... 1007 wyśw. 27-11-2020 17:06

1f/81 Kurs Maturalny Rozszerzony

Udowodnij, że dla każdej liczby pierwszej ,,k'' większej od 3 liczba (k-1)^2(k+1)^2 jest podzielna przez 576.


Pytanie 1. Czy takie rozwiązanie jest w 100% poprawne?

Pytanie 2. Czy dobrze rozumiem, że liczbę pierwszą ,,k'' mogę przedstawić jako liczbę niepodzielną przez 3 dlatego ponieważ, każda liczba pierwsza większa od 3 zawiera się w liczbach niepodzielnych przez 3?
No bo inaczej jeżeli m należy do liczb całkowitych, to dla ,,m''=0 , k=1 co jest sprzeczne z założeniem.
Jeżeli mój tok rozumowania jest poprawny to proszę o potwierdzenie.

Pytanie 3. Czy przy rozważaniu liczby pierwszej ,,k'' w dwóch podzbiorach , liczba ,,m'' ma należeć do całkowitych czy naturalnych? Czy jest to bez znaczenia?

Dowodzenie podzielności Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski 29-11-2020 08:21

Pyt. 1: tak, w 100% poprawne. Brakuje mi jednak w samym rozwiązaniu informacji, że liczba pierwsza k nie może być podzielna przez 3, zatem rozpatrujesz ją jako 3k+1 lub 3k+2. 

Pyt. 2: poprawne rozumowanie.

Pyt. 3: powinno do naturalnych, ale napisanie, że do całkowitych nie będzie błędem (zbiór liczb naturalnych zawiera się w całkowitych).

... 31-01-2021 20:13

A jeszcze mnie naszła taka myśl: 

jarosinski 31-01-2021 22:14

Wniosek z równoważnym przekształceniem tezy jest poprawny (z resztą w oparciu o ten wniosek układałem treść tego zadania). Wniosek będzie prawdziwy w przypadku liczb całkowitych (czyli np. 400 | x^2  <-> 20|x)

... 31-01-2021 22:34

Czyli dobrze rozumiem, że w każdym z poniższych przypadków przypadków, jeżeli, dana liczba np. ,,k'' należy do liczb całkowitych to zawsze mogę pominąć wartość bezwzględną?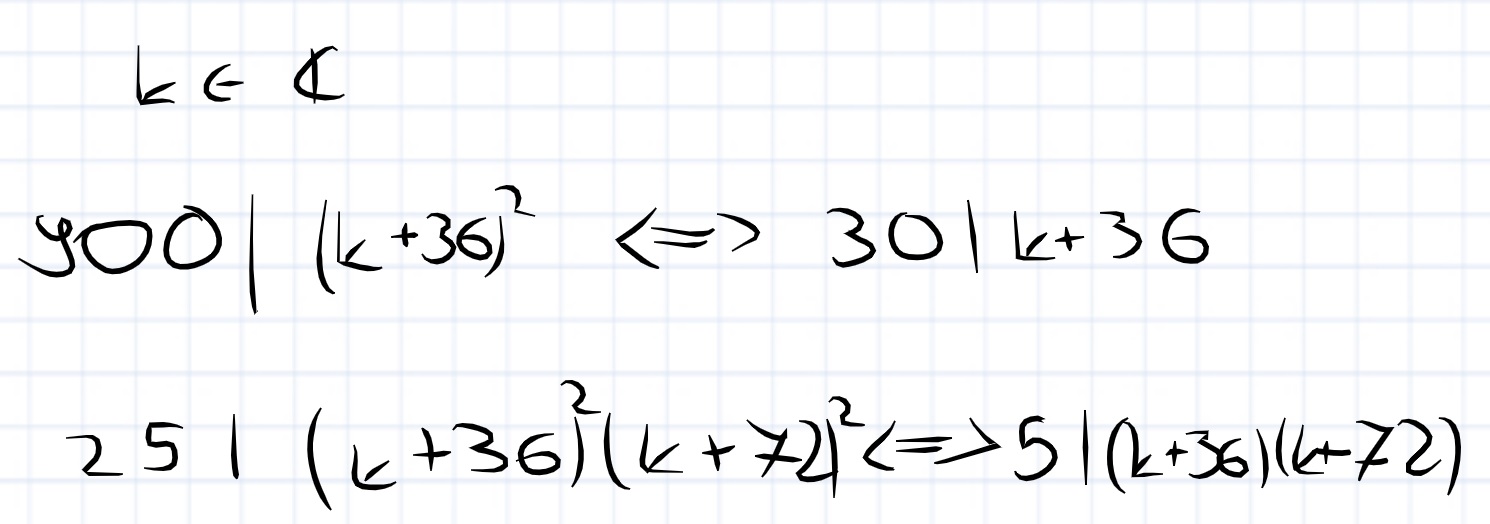

jarosinski 02-02-2021 08:57

Tak, to dobre rozumowanie.