2016s2.3/60 Kurs maturalny fizyka

W zasadzie nie ma tutaj innego wyjścia jak przyjęcie, że v1 = v2, czyli prędkość liniowa krążka jest taka jak obciążnika - jest to zresztą racjonalne rozumowanie, zakładając, że linka się nie rozciąga ani nie staje się "luźna". W rzeczywistości ta linka owijałaby się jeszcze wokół krążka i zapewne to założenie nie byłoby do końca prawdziwe, ale nie mamy za bardzo innego wyjścia. Co do prędkości kątowej, to zawsze można ją wyrazić przez prędkość liniową i promień: a zatem w = v2/r, gdzie r to będzie promień tego dużego walca. W efekcie jedyną niewiadomą jaka nam pozostanie będzie v1, które chcemy wyliczyć.

Panie Guguła, czy obliczajac energie ruchu postepowego krazka napewno mozemy wziasc pod uwage sume predkosci ruchu obrotowego i postepowego jako "v" bez wyrozniania tych predkosci? 

Hmm, nie wiem czy rozumiem pytanie, ale w każdym razie my zapisując tutaj energię kinetyczną ruchu postępowego krążka wcale nie zapisujemy jego prędkości jako jakiejś sumy dwóch różnych prędkości, tylko jest to jedna prędkość, związana tylko z ruchem postępowym krążka, czyli v2 (według oznaczeń koleżanki z pierwszego posta w tym temacie). Natomiast w energii związanej z ruchem obrotowym mamy omegę, którą możemy rozpisać akurat jako omega = v2/r, bo skoro toczenie jest bez poślizgu, to oznacza to, że prędkość w ruchu obrotowym każdego punktu na "obwodzie" tego dużego walca jest równa prędkości ruchu postępowego środka masy.

Dajmy na to, że środek walca porusza się z jakąs predkościa v(post). czy zatem zgodnie z rysunkiem kolegi Szymona w puncie gdzie przyczepiona jest linka prędkośc linki nie bedzie wynosila v(post)+omega*R? I jeżeli tak to czy do rownania prędkości w ruchu postępowym walca nie powinniśmy przyjmować v(post) jedynie środka walca?

Ale czym jest "równanie prędkości w ruchu postępowym walca"? Bo w tym zadaniu należy wykorzystać zasadę zachowania energii mechanicznej (zapisaną w pierwszym komentarzu autorki tematu) i tam w istocie w miejsce prędkości ruchu postępowego walca wstawiamy tylko to co Ty oznaczyłeś jako v_post (czyli v2 = v_post), bo to jest właśnie prędkość ruchu postępowego środka masy walca. Nie wstawiamy tam żadnego v_post + omega*R.

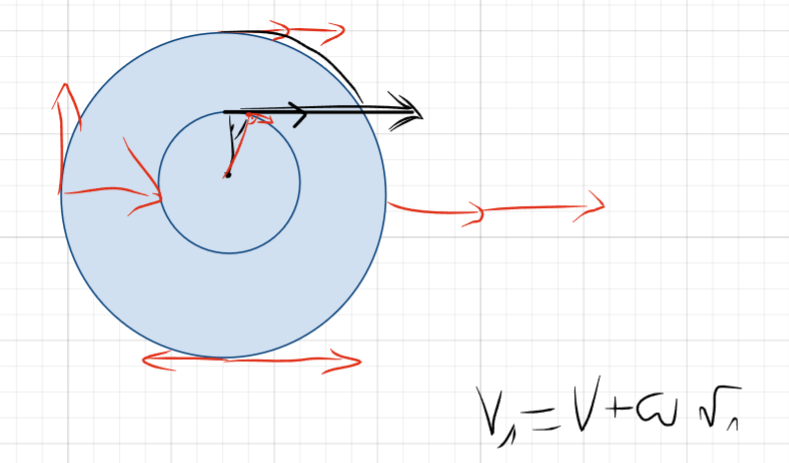
Tak tak musimy wstawić v(post), zastanawiam się tylko czy aby na pewno v(post) jest równe v z jaką spada bloczek. Wydaje mi się że v bloczka jest złożeniem v(post) i omega*r (bo przecież v(post) = omega*R tylko na obrzeżach walca).

Tzn. my tu musimy poczynić jakieś założenia, bo jak dla mnie niestety treść tego wyraźnie nie doprecyzowuje, dlatego takim naturalnym podejściem jest przyjęcie (co napisałem w pierwszej mojej odpowiedzi na oryginalne pytanie), że linka ani się nie rozciąga, ani nie staje luźna, ani się nie owija wokół walca, ani się nie rozwija, więc zakładamy, że odległość między środkiem masy walca jest a opadającym ciężarkiem (liczona wzdłuż nici) jest stała. A to oznacza, że v opadającego ciężarka = v(post) środka masy walca.

Natomiast masz rację pisząc, że faktycznie mogłoby być tak, że prędkość opadającego bloczka byłaby nieco większa niż prędkość v(post) środka masy walca, bo przecież mogłoby dojść do takiej sytuacji, że ta linka się nieco rozwija i wtedy odległość między ciężarkiem a walcem się zwiększa, więc w istocie v(ciężarka) > v(post) walca. Natomiast samo CKE zakłada, że te prędkości są takie same w swoich rozwiązaniach (ale powinno to zostać w treści jakoś doprecyzowane). Można to też usprawiedliwić tak, że zakładamy tylko bardzo krótki początkowy przedział czasu, w którym możemy przyjąć, że w pewnym bardzo dobrym przybliżeniu te prędkości są sobie bardzo bliskie.