zadanie 12 z próbnej matury 2020 Operon
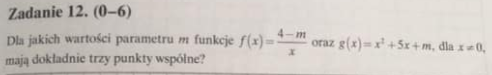
O to chodzi w tym zadaniu, żeby przyrównać funkcje do siebie i wyznaczyć wzory viete'a do 3? Czy o coś innego
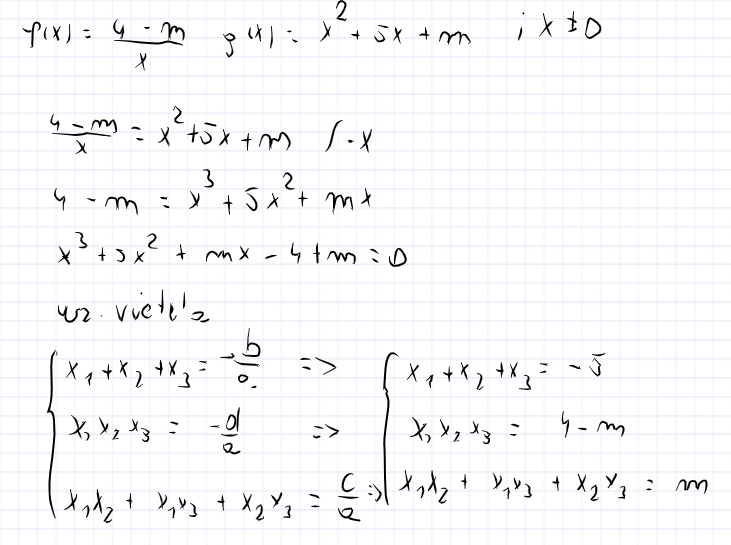
wielomian Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Podaj jakiś kontakt to ci wyśle, niektóre szkoły już dostały,
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Podrzucam maila: [email protected]
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
wysłałem, sprawdź sobie, zdjęcia trochę niewyraźne ale niestety nie mam innych
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Niestety ale nie moge znaleźć , wiadomości nie ma ani na poczcie głównej ani na spamie ://
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
[email protected] (ewentualnie ten mail bo mozliwe ze tamta poczta kuleje)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Już tu wstawiłem, ale wysle ci jeszcze raz na maila, a tutaj innym się pewnie przyda
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czy w tym zadaniu nie chodzi o to aby zauważyć, że W(-1)=0 więc (x+1)(x^2+4x-4+m)? I nastepnie postawić warunki na dwa pierwiastki z drugiego nawiasu, że x2, x3 różne od x1 =-1?
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@dp1, tez to zauważyłem grupując wyrażenie wyciągając (x-1) przed wyrażenie, ale na maturze bym pomyślał raczej właśnie o tych wz. viete'a i stąd moje pytanie, czy da się nimi to zadanie zrobić
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tego typu zadań raczej nie wykonuje się ze wzorów Viete'a dla wielomianu trzeciego stopnia ze względu na bardzo trudny układ równań do rozwiązania. To zadanie można zrobić dwoma metodami:
1) zauważyć, że liczba -1 jest pierwiastekiem wielomianu uzyskanego po przekształceniach
2) doprowadzić do równania m=g(x) (czyli separacja zmiennych) i zastosować rachunek różniczkowy- czyli z przebiegu zmienności funkcji narysować ją i odczytać rozw.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych

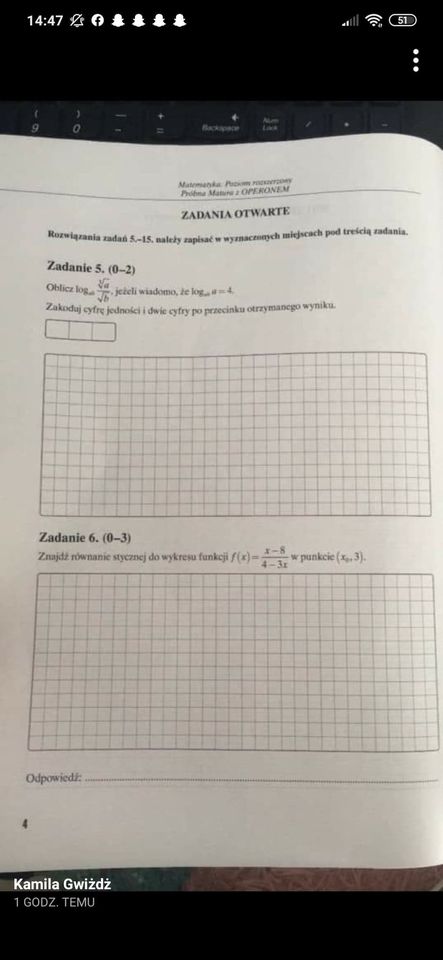

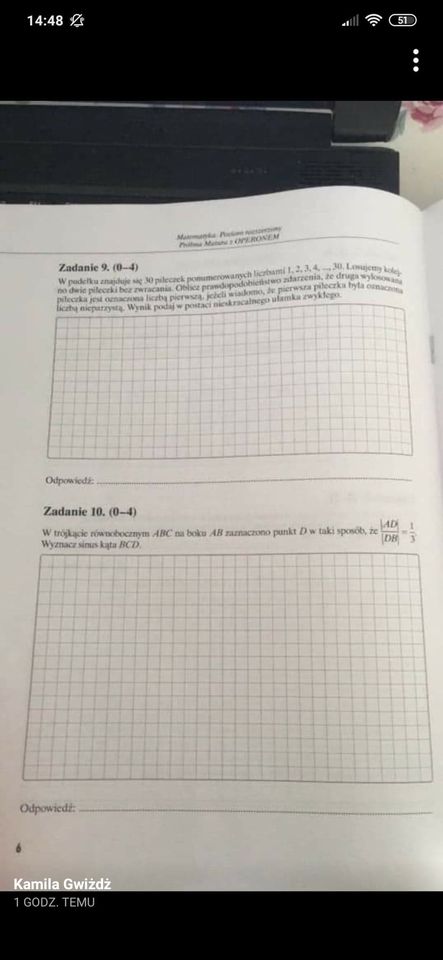




Ciekawe zadanie, wydaje mi się właśnie, że skoro mają być 3 punkty to powinno coś wyjść z wzorów Viette'a , wie ktoś apropo skąd istnieje możliwość uzyskania arkuszu próbnego? Bo niestety dostaniemy go w naszej szkole dopiero po powrocie..