Anonim 1392 wyśw. 02-12-2020 13:36

2019.N.4

Wskaż zbiór wszystkich rozwiązań równania |cosa+cos3a+cos5a|=3

a) a:a=n*60, n jest dowolną liczbą całkowitą

b)a:a=n*90, n jest dowolną liczbą całkowitą

c)a:a=n*190, n jest dowolną liczbą całkowitą

d) a:a=n*360,n jest dowolną liczbą całkowitą

Z własnosci funkcji cosinusa wiem, że przyjmuje on wartości należące <-1;1>, rozpisałam moduł: cosa + cos3a + cos5a = 3 lub cosa + cos3a + cos5a = -3. Z pierwszego równania wychodzi, że każdy cos musi być równy 1, a z drugiego każdy cos musi być równy -1.

Czyli z pierwszego równania : a=2kpi i 3a=6kpi i 5a=10kpi ---> każdy kolejny cos(n*a) zmienia się o 2kpi

Z drugiego równania: a=pi+2kpi i 3a=3pi+6kpi i 5a=5pi+10kpi ----> każdy kolejny cos(n*a) zmienia się o pi+2kpi

Czy dobrze to rozumiem? Jeśli tak, to jak dalej to interpretować?

Matematyka Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
Grzegorz.p7 02-12-2020 14:30

Myślałeś dobrze, ale nie możesz oznaczyc wszystkich 3 równań jako kpi, w każdym musi być inna literka


Anonim 02-12-2020 14:58

Drugi przypadek to będzie:

a=pi+2kpi i 3a=pi+2lpi i 5a=pi+2mpi  ; k,l,m, należace do C

czyli a=pi+2kpi i 3pi+6kpi=pi+2lpi i 5pi+10kpi=pi+2mpi

czyli a=pi+2kpi i 2pi(1+3k-l)=0 i 2pi(2pi+5k-m)=0

?

Grzegorz.p7 02-12-2020 15:10

wszystko dobrze tylko w ostaniej linijce wychodzi, że l = 3k +1, m = 5k+2 czyli z tego wychodzi, że alfa = pi +2kpi

PS. wcześniej żle ci napisałem bo podałem że alfa = kpi zamiast alfa =2kpi, ale odpowiedzi to nie zmienia bo, z 1 warunku mamy parzyste wielokrotności 2pi, czyli 2pi; 4pi; 6pi, a z tego warunku nieparzytse wielokrotności 2pi, czyli pi; 3pi, 5pi itd.

czyli po zsumowaniu to alfa = kpi

Anonim 02-12-2020 15:15

W jaki sposób znika 2pi w ostatniej linijce? Tam przy wyliczeniu l i m

Grzegorz.p7 02-12-2020 15:21

tutaj masz dla l, dziele przez pi(bo wiem ze to nie zero tylko okolo, 3,14)


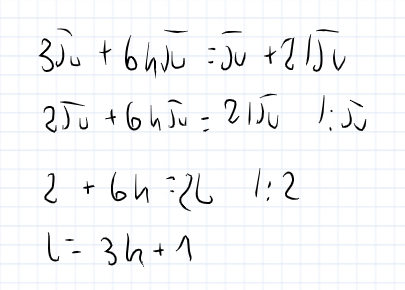
Anonim 02-12-2020 15:24

Dzięki wielkie za pomoc!