1f/82, Kurs maturalny rozszerzony
Rozwiąż nierówność,
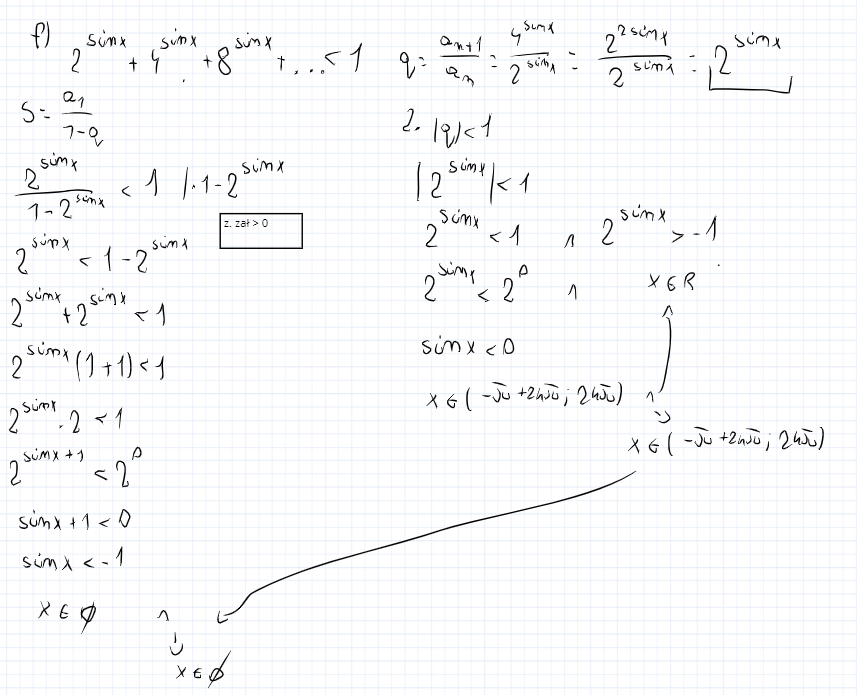
2^sinx+4sin^x + 8sinx +... < 1
Odpowiedz koncowa mi wyszła ze x nalezy do zbioru pustego, ale dlaczego mi wychodzi odrazu z równania, że x nalezy do zbioru pustego, a w odpowiedziach do jakiegoś przedziału?
szereg Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Przepraszam nie popatrzyłam na założenia
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
ja postawiła t i wyszło mi tak
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
widziałem własnie ze niektórzy podstawiają t, ale skoro jest to szereg i dałem założenie ze mianownik jest większy od zera to mogę pomnożyć przez niego, a potem wydaje mi się, że wszystko dobrze liczę
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Problem jest w przemnazaniu, bo zauważ że jeżeli przerzucisz 1 na lewo to nawet bez podstawami wyjdą ci dwa wyniki. Niestety nie mogę wyczaić dlaczego jest to błąd ://
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Myślę, że może być to spowodowane tym, że i tak wychodzi zbiór pusty, więc stąd wychodzi od razu taka odpowiedź, ale nie wiem, na pewno można pomnożyć, bo moje założenie to gwarantuje, cóż może ktoś będzie potrafił to wyjaśnić o co dokładnie tutaj chodzi,
Ogolnie to nie wiem ile pkt moge sobie przyznac
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Myślę, że to dobry moment, żeby Pan Jarosiński się wypowiedział na ten temat :D
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ja doszedłem dokładnie do tego samego co Ty
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jeśli się pomnoży razy kwadrat mianownika to wychodzi rozw. z kryteriów, a jeśli razy mianownik to zbiór pusty. I nie jest to błędem bo suma sumarum, robiąc część wspólną z założeniem w obu przypadkach rozwiązaniem jest zbiór pusty.
Ps. Przypominam, że nierówność z szeregiem zawsze można pomnożyć razy mianownik, ponieważ przy założeniu zbieżności szeregu, zawsze on jest z przedziału (0 ; 2).
- 3
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A czy nie powinno być, że z przedziału (0,1)?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie, nie powinno być ponieważ jeżeli q należy do przedziału (-1;1). Czyli jeżeli będziesz miał (1-q) to możesz sobie wyobrazić że będzie 1-(1)=2 lub 1-1=0 (natomiast nigdy nie osiąga wartości -1 i 1 więc będzie od (0;2)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie możesz pomnożyć razy 1-2^sinx musisz to pomnożyć jako kwadrat tego wyrażenia (1-2^sinx) ^2