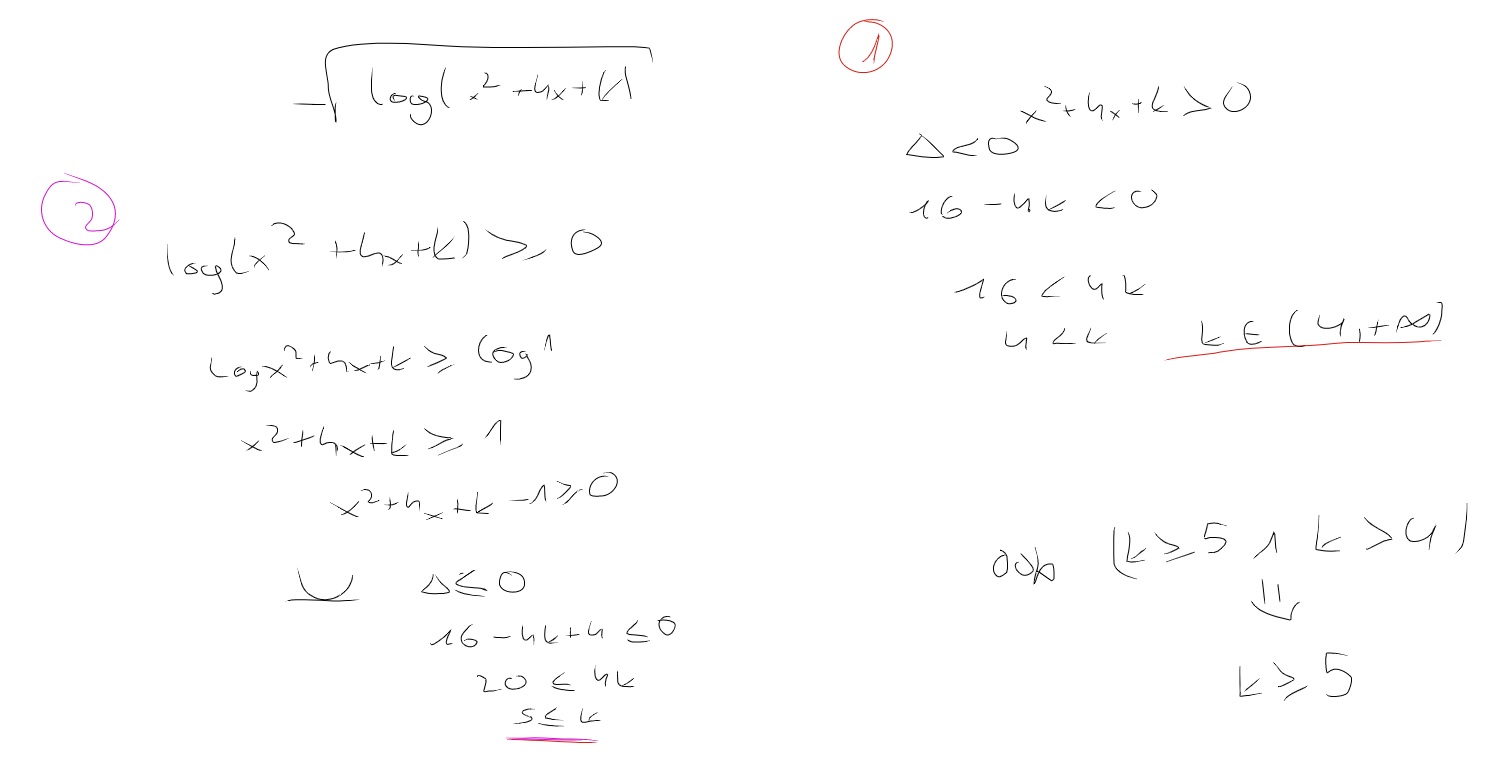zad 499/91, Kiełbasa I
Wyznacz te wartośći parametru m, dla których dziedziną funkcji f(x) = pierwiastek z log(x^2 + 4x + k) jest zbiór liczb rzeczywistych
Mogłby mi ktoś rozpisać to zadanie z dokladnym wyjaśnieniem? Robie to zadanie ale wychodzi mi zly przedział.
To co pod pierwiastkiem powinno byc nieujemne i (x^2+4x + k) > 0 z jednocześnie delta mniejsza od zera?
logarytmy Dodaj post do ulubionych Poproś o pomoc
Mam do ciebie pytanie bo nie mogę sobie tego zobrazować, pierw dajemy warunek np że, jest to większe od zera, a potem liczymy delte, i zapominamy o warunku, że ma być to większe od zera? czy jak to działa, nie mogę tego właśnie zrozumieć
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jeżeli dobrze zrozumiałem pytanie, z dziedziny log otrzymujemy, że takie równanie kwadratowe > 0. Takie równanie możemy sobie zobrazować jako zwykła funkcja f(x). Z treści zadania masz dane że dziedzina x musi być R. Więc nie interesuje cię czy w tej nierówności jest jakiś przedział, itp, masz obliczyć kiedy ta funkcja ZAWSZE będzie większa od 0 (dla danego parametru) <=> delta<0, bo a>0. Daj znać czy o to ci chodziło.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych