8.23 Kłaczkow
W trójkącie 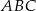 poprowadzono prostą
poprowadzono prostą 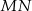 równoległą do prostej
równoległą do prostej 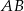 tak, że
tak, że 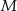 należy do
należy do 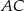 ,
, 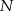 należy do
należy do 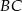 oraz
oraz 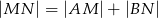 . Oblicz
. Oblicz 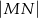 , jeśli
, jeśli 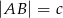 , a miary kątów trójkąta przy boku
, a miary kątów trójkąta przy boku 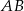 wynoszą
wynoszą  oraz
oraz 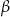 .
.
Hej. Mógłby mi ktoś wytłumaczyć to zadanie? Nie chodzi mi o samo rozpisanie, tylko wytłumaczenie ponieważ tego nie rozumiem.
planimetria Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1) tw. sinusów z trójkąta ABC (między bokami a, c oraz sinusami odpowiednich kątów) - dostaniesz z tej zależności bok a
2) tw. sinusów z trójkąta ABC - (między bokami b, c oraz sinusami odpowiednich kątów) - dostaniesz z tej zależności bok b
3) zauważasz, że trójkąty MNC (tu na kartce mam zapis błędny NNC :), powinno być MNC) oraz ABC są podobne - cecha kkk - to pozwala wyznaczyć skalę podobieństwa k w zależności od boków, potem w zależności od obwodów, w obwodzie trójkąta MNC musisz coś zauważyć z rysunku
4) przyrównujesz obie skale do siebie, wychodzi ci zależność, z której możesz wyznaczyć x, czyli u mnie |MN|, później wystarczy tylko podstawić do wzoru a i b wyliczone w punkcie 1 i 2. Na koniec upraszczasz