8.30/132 Kłaczkow
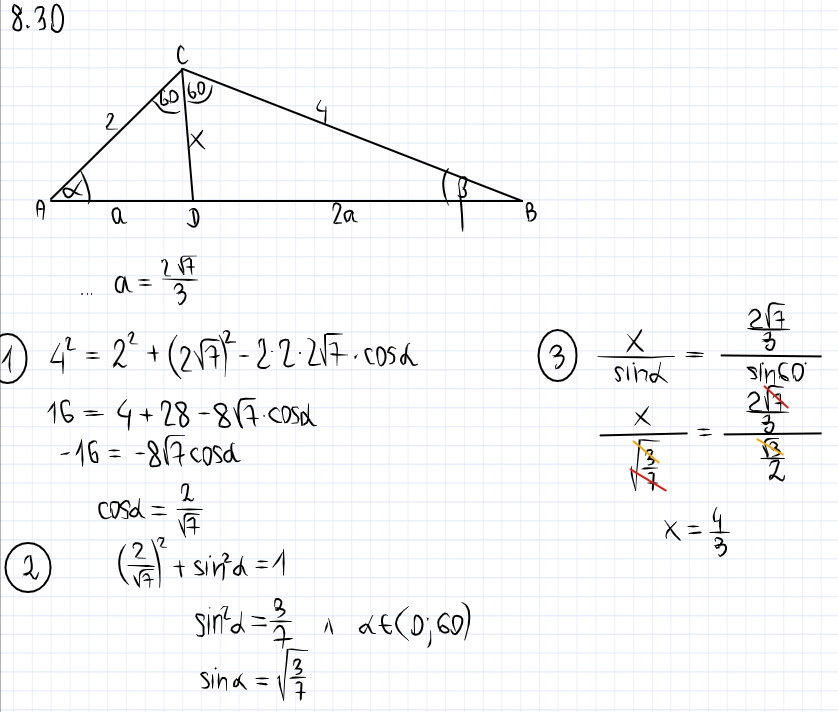
W trójkącie ABC dane są : BC=4cm AC=2cm , <ACB=120. Wyznacz długość dwusiecznej kąta ACB zawartego w tym trójkącie.

planimetria twierdzenie sinusów i cosinusów. Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Uloz drugie rownanie z twierdzeniem cosinusow dla trojkata CBD. Wyjdzie ci wtedy x = 4/3 lub 8/3. Czyli jedynym x ktory spelnia te dwa rownania jest 4/3. Tutaj poszedles na latwizne troche I ulozyles rowanie, a powinien to byc uklad rownanian, z jedna niewiadoma zlozony wlasnie z dwoch twierdzen cosinusow.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1) sprawdzić otrzymane wyniki lub dać założenia np, że bok naprzeciwko największego kąta musi być największy itd
2) sprawdziłem wynik używając szacowania
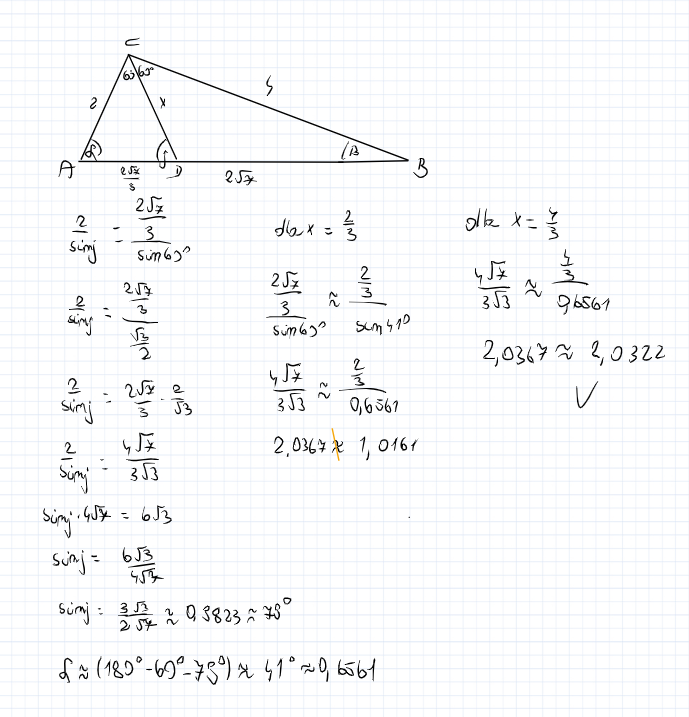
Pierw obliczyłem przybliżoną wartość kąta przy wierzchołku D, to mi pozwoliło podać przybliżoną wartość przy wierzchołku A, kąt wyszedł około 41 stopni. Rozpatrzyłem dwa przypadku dla x = 2/3 i dla x = 4/3, i sprawdziłem to znów z twierdzenia sinusów, dla x =2/3 wyszła ogromna różnica, więc nie jest to możliwe ze x = 2/3, ale już dla x =4/3 wyszedł bardzo podobny wynik wiec x = 4/3.
Nie wiem czy jest to poprawny sposób rozwiązania, ale że mi wyszło postanowiłem przedstawić ten sposób
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@Grzegorz.p7
Ad1) ale "bok naprzeciwko największego kąta musi być największy"- jest spełnione dla obu rozwiązań.
Ad 2) jest ok
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@Jarosiński, tak wiem ale chodziło mi ogólnie jakie można dać założenia do zadań, żeby zorientować się, któe rozwiązanie jest niepoprawne(w tym zadaniu również to sprawdziłem i nic nie dało tak jak Pan mówi. Wypisałem to bo często przez to można odrzucić jakieś rozwiązanie
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Moje odp na powyższe pytania:
1) w trójkącie ADC mamy 3 informacje, zatem istnieje tylko jeden trójkąt o wskazanych parametrach. Stąd wynika, że nie może być dwóch różnych wartości x
2) wyrzucamy 2/3- można np. wykonać sprawdzenie z twierdzenia cosinusów w trójkącie BCD
3) najlepiej użyć równania liniowego czyli tw. sinusów, a nie kwadratowego jak twierdzenie cosinusów (które może wygenerować dwa rozwiązania):
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jeżeli zapiszesz równanie dla drugiego trójkąta BCD otrzymasz także równanie z kwadratowe z x^2 podstawiając je do siebie uzyskasz równanie liniowe. Przez co nie będziesz musiał liczyć kwadratowego i otrzymasz jedno rozwiązanie.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Bardzo dobre pytanie na które znam odpowiedź. Ale chciałbym, żebyście wy też pogłówkowali. Rozszerzę zatem naszą zagadkę do trzech pytań:
1) skąd na maturze uczeń ma wiedzieć, że jedno z rozwiązań jest niepoprawne? Tutaj wiecie bo są odp, ale na maturze jak się zorientować?
2) które rozwiązanie i dlaczego odrzucić?
3) jak to rozwiązać inaczej żeby uniknąć takiego problemu? Jaka metoda / narzędzie?