przykład z lekcji
Suma wszystkich czterech współczynników wielomianu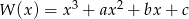 
jest równa 0. Trzy pierwiastki tego wielomianu tworzą ciąg arytmetyczny o różnicy równej 3. Oblicz współczynniki 
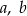i 
. Rozważ wszystkie możliwe przypadki.
W tym przykładzie Pan Jarosiński stosował wzory Viete'a jednak nie do końca potrafię zrozumieć skąd bierze się ten układ równań:
a=-3r-9
b=3r^2+18r+18
c=-r^3-9r^2-18r
1+a+b+c=0
Wiem, że postać iloczynowa wielomianu wygląda tak:
W(x)=(x-r)(x-r-3)(x-r-6)
Czy mógłby ktoś raz jeszcze wytłumaczyć skąd bierze się wyżej wspomniany układ równań? Oglądałem nagranie z lekcji już dwukrotnie, nie potrafię tego zrozumieć a Pan Jarosiński wspominał, że jest to bardzo ważne.
wielomiany Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
wyjdzie to samo tylko ja mam inne oznaczenia, a = 1 bo to wiem z polecenia, przy x^3 stoi 1 czyli moje a,
to jak w funkcji kwadratowej np x^2 -4x + 6, to moje a = 1, b = -4, c = 6
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
aa okej, dziękuję za pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
korzystamy z wzorów viete'a dla wielomianu 3 stopnia(które możesz pamietać na pamięć, lub je wyprowadzić, robił to Pan na tej samej lekcji, ja raczej wole pamiętać, bo to dodatkowy czas), z postaci iloczynowej znamy miejsca zerowe stąd podstawiamy pod wzory i liczymy współczynniki b,c,d