8/83 zadanie domowe
Na trapezie o podstawach a oraz 2a i wysokości a opisano okrąg. Oblicz odległość środka tego okręgu od wszystkich jego boków.
Mam 2 pytania do tego zadania:
1) Czy tutaj należy obliczyć odległości od środka okręgu do środka każdego boku?
2) Zrobiłam to zadanie na podstawie tego co jest w pierwszym pytaniu i jeśli jest to dobrze, to jak obliczyć odcinek oznaczony na moim rysunku jako x?
*w następnej linijce na zdjęciu obliczyłam jeszcze |OH|=a-z=7a/8

matematyka Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A czy zawsze w zadaniach tego typu liczymy odległość od środka okręgu do środka boku? Bo można połączyć środek okręgu z innym dowolnym punktem zawierającym się w boku.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jakbyś połączyła wierzchołek A i C to powstał by ci trójkąt, na którym ten okrąg był by opisany.
I z twierdzenia poznanego na lekcji: Środek okręgu opisanego leży na przecięciu się symetralnych, z tego wynika że jeżeli masz trapez wpisany w okrąg (zawsze równoramienny btw) to zawsze łączysz ze środkiem boku, co więcej pod kątem prostym.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Odpowiadając na pytanie 1: odległość punktu od odcinka liczymy jako najkrótszą odległość pomiędzy nimi, czyli pod kątem prostym (na rysunku jest do "d"). Ogólnie jest to coś innego niż odległość punktu od środka odcinka (na rysunku "x"). Ale w przypadku tego konkretnego zadania jest to to samo.
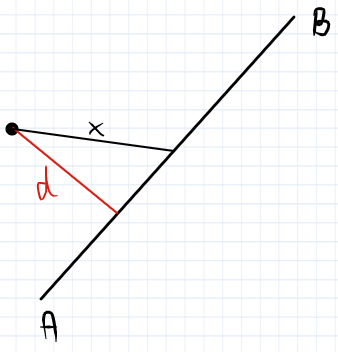
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
x jest to wysokość trojkata rownoramiennego OBC (miedzy innymi) wiec nalezy obliczyc go z tw pitagorasa np w trojkącie OFC.
A odp na 1 pyt: No tak w tym przypadku jest to środek tego boku bo wysokość w trojkącie rownoramiennym dzieli podstawe na poł :)