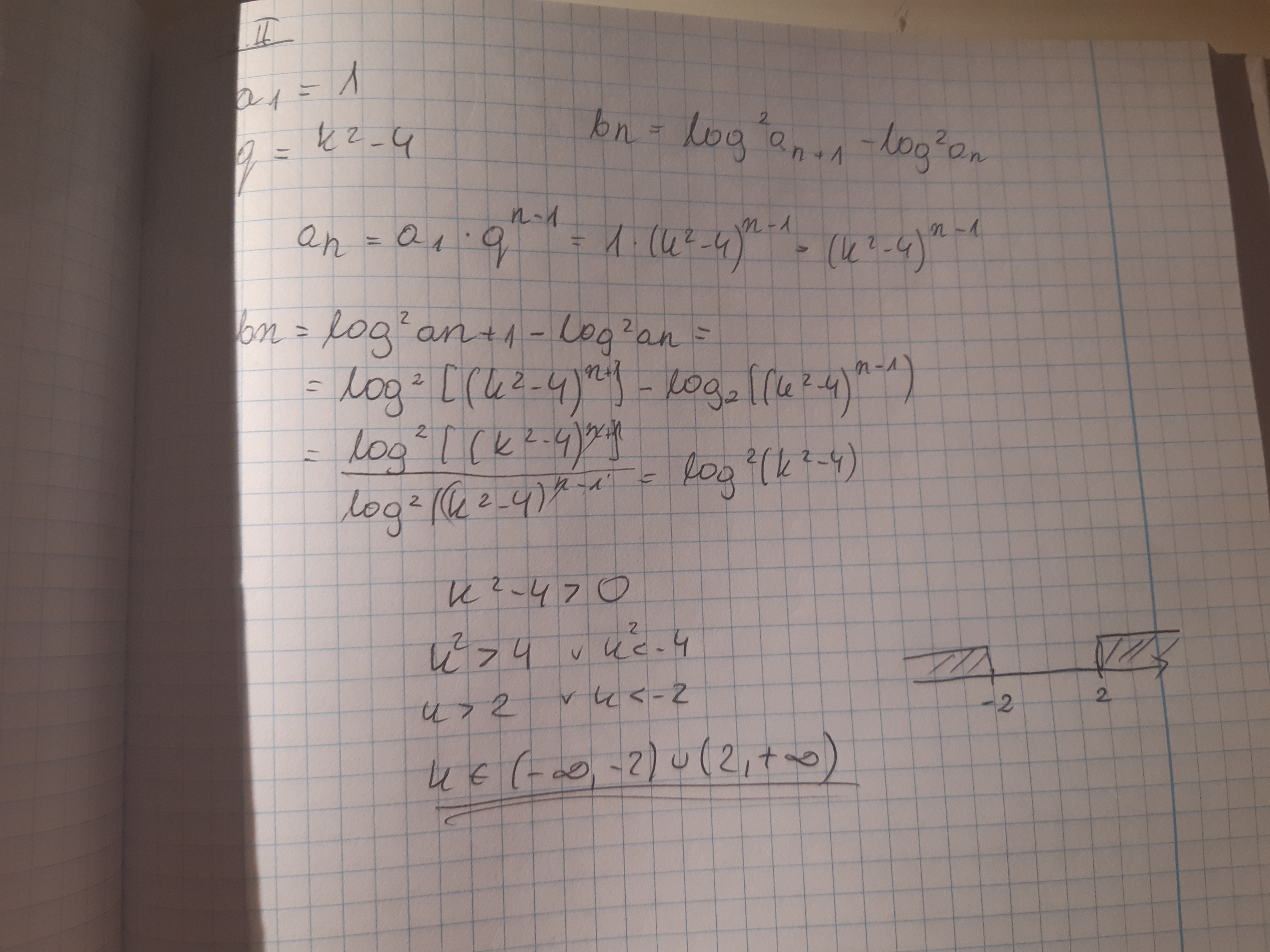pj20 720 wyśw. 16-01-2021 14:02

1 cz II / 85 Kurs maturalny rozszerzony

Pierwszy wyraz i iloraz ciągu geometrycznego an wynoszą odpowiednio 1 i k^2 - 4. Zbadaj dla jakich wartości parametru k ciąg bn o wyrazie ogólnym bn = log^2(a n+1) - log^2 (an) jest ciągiem arytmetycznym. 

Mógłby ktoś pokazać mi swoje obliczenia?

matematyka Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
karo022 17-01-2021 16:33



<3 19-01-2021 17:32

Skąd wiemy, że ciąg bn będzie akurat arytmetyczny, w nie np jakiś przypadkowy ciąg? Nie powinnismy jeszcze udowodnić ze różnica jest stała? 

jarosinski 14-02-2023 14:00

My szukamy takich wartości arametru dla których ten ciąg będzie arytmetyczny. Wynika to z polecenia. Arytmetyczny będzie wtedy gdy różnica będzie stała.