2011C.5.8

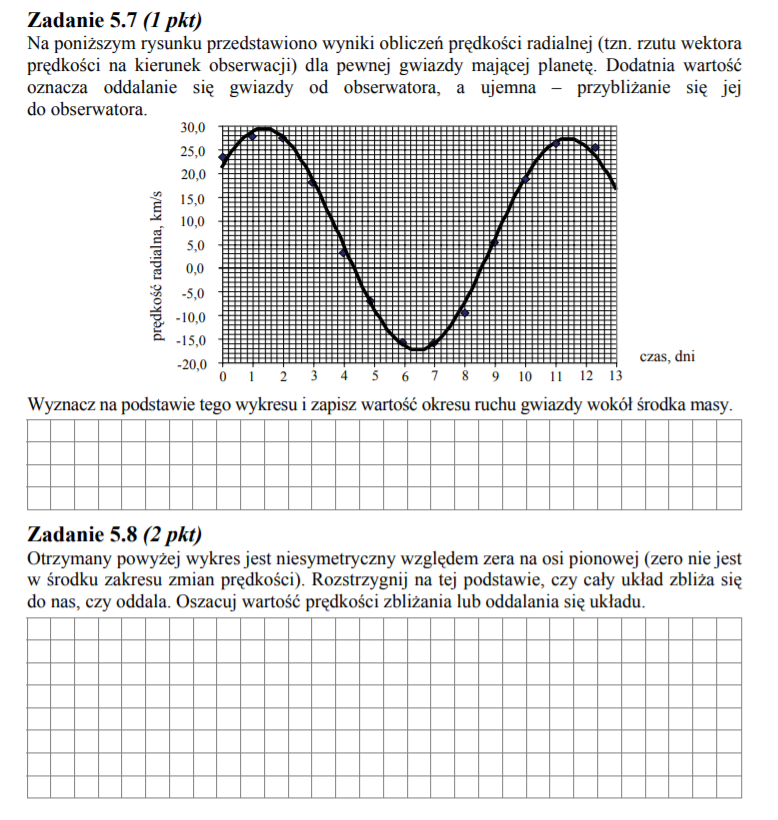
Warto zerknąc tu na dodatkową informację do tego zadania (str. 276 w naszym podręczniku) - mówi nam ona, że rozważany układ to gwiazda-planeta, które krążą po okręgu wokół wspólnego środka masy. Gdyby zatem ów ukłąd nie oddalał się od obserwatora, to amplituda mierzonej prędkości gwiazdy musiałaby być taka sama w kierunku od obserwatora (wartości dodatnie na wykresie) jak w kierunku do obserwatora (wartości ujemne), bo to zwyczajny ruch po okręgu z prędkością o stałej wartości, a zatem na zamieszczonym wykresie nie byłoby tej asymetrii. Asymetria jednak jest - widzimy przesunięcie w stronę dodatnich wartości, co oznacza, że cały układ musi mieć jeszcze jakąś prędkość względem obserwatora, a ponieważ daje ona dodatkowy wkład w dodatnie wartości na wykresie, to musi to być oddalanie się (kierunek od obserwatora).

Prędkość oddalania można oszacować jako wartość tego przesunięcia wykresu w górę, np. widać że amplitudy prędkości wynoszą odpowiednio dla kierunku od obserwatora i kierunku do obserwatora ok. 30 km/s i 18 km/s. Przesunięcie wynosi zatem ok. 6 km/s (gdyby go nie było to obie amplitudy osiągałyby wartość równą około 24 km/s), a zatem taka jest prędkość oddalania się tego ukłądu od obserwatora.

Dziękuję bardzo!