Koala 710 wyśw. 24-01-2021 17:25

zz89.2/110 Kurs maturalny fizyka


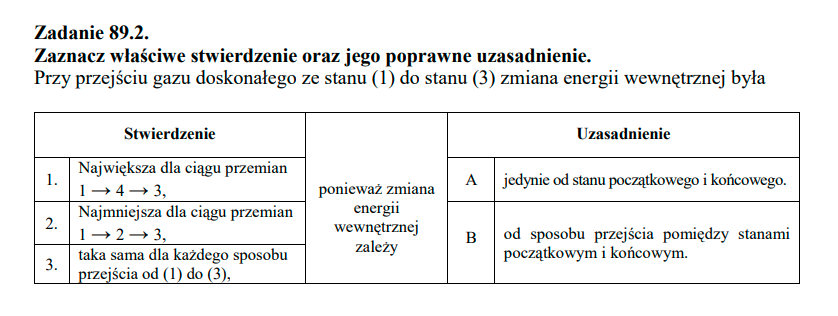
Skąd mamy zależność która się pojawia w kluczu U=3/2pV? I czy można też wywnioskować odpowiedź na podstawie wzoru U=CpndeltaT, więc można wywnioskować, że energia wewnętrzna zależy od początkowego i końcowego stanu?

fizyka Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
s.gugula 26-01-2021 14:33

Ten wzór U = (3/2)*p*V bierze się dokładnie z tego wzoru, który miałaś na myśli, czyli deltaU = n*Cv*deltaT (tam jest deltaU a nie samo U i nie Cp tylko Cv ;)). Możemy bowiem rozwinąć ten wzór wiedząc, że dla 1-atomowego gazu Cv = 3/2 R, a zatem: deltaU = (3/2)*n*R*deltaT, przechodząc ze zmian wielkości na same wielkości, dostajemy U = (3/2)*n*R*T, a z prawa Clapeyrona mamy p*V = nRT, a zatem podstawiając to do poprzedniego wzoru dostajemy U = (3/2)*p*V. A zatem Twoje podejście jest niejako tym samym, które zostało zastosowane w odpowiedziach, przy czym w tym przypadku jak najbardziej wystarczające byłoby użycie wzoru deltaU = n*Cv*deltaT i wywnioskowanie z niego, że faktycznie energia wewnętrzna zależy od stanu początkowego i końcowego (a ściślej od temperatury tych stanów).