ADRYAN11 841 wyśw. 24-01-2021 20:23

Kurczab 3.120/93

Przekształcenie P określone jest wzorem P((x,y)) = (y+2, -x+1), gdzie x,y€R

a)wykaż, że przekształcenie P jest izometrią

Nie rozumiem tego przekształcenia. Sadziłem, że przekształcenie y+2 to będzie zwyczajnie symetria względem OY i później przesunięcie o wektor [0,2] (rozpisałem to niżej), ale okazuje się że tak nie jest.
Sprawdziłem odpowiedzi i okazało się, że współrzędne punktu zwyczajnie zamieniaja się w samo przekształcenie, czego kompletnie nie rozumiem. Wytłumaczy mi to ktoś? :)

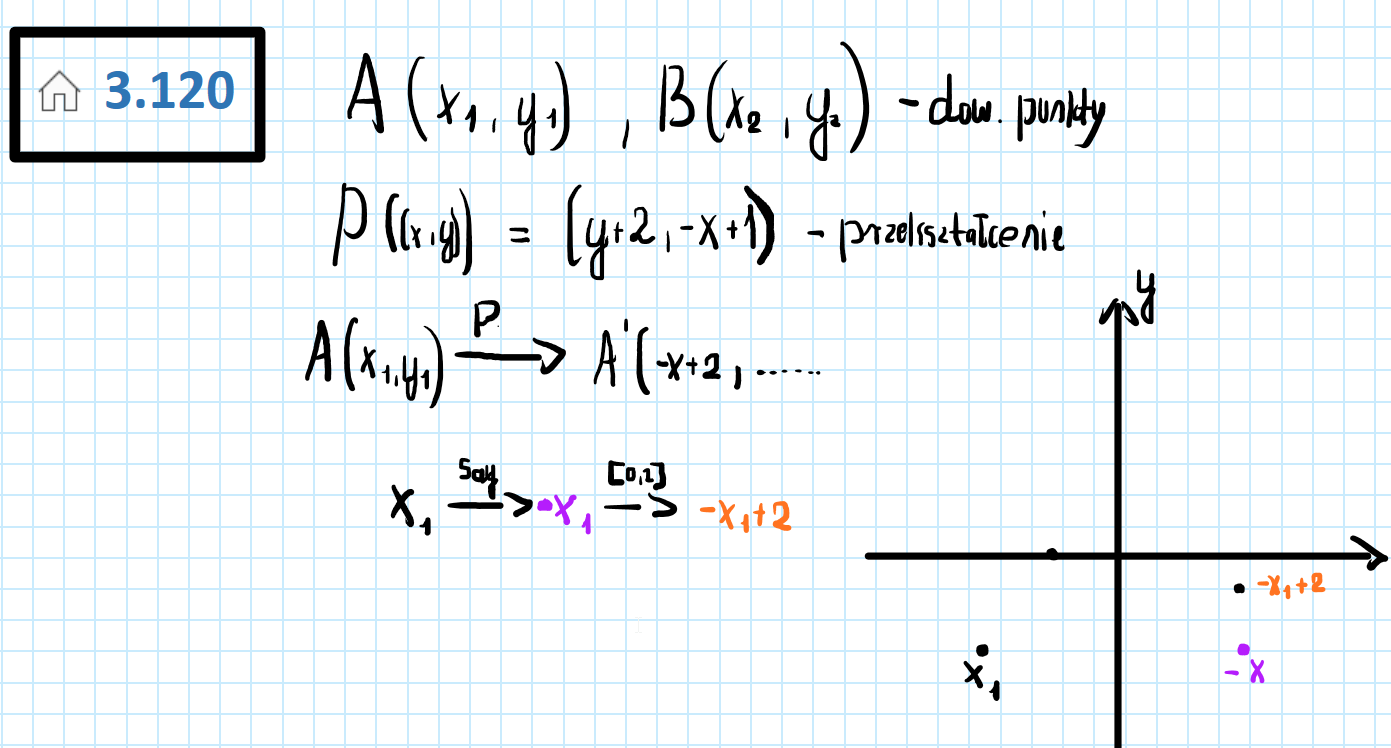
przekształcenia geometria analityczna Dodaj post do ulubionych Poproś o pomoc

jarosinski 26-01-2021 10:03

Weźmy dwa punkty: $P_{1} = (x_{1}, y_{1}) \Rightarrow P_{1}^{'} = (y_{1} + 2, x_{1} - 1)$ oraz $P_{2} = (x_{2}, y_{2}) \Rightarrow P_{2}^{'} = (y_{2} + 2, x_{2} - 1)$

Jeżeli więc w pewnym przekształceniu odległość między dowolnymi punktami figury jest taka sama jak odległość obrazów tych punktów, to mamy do czynienia z przekształceniem izometrycznym (izometrią) Zatem przekształcenie jest izometrią jeśli zachodzi: $| P_{1} P_{2} | = | P_{1}^{'} P_{2}^{'} |$

$| P_{1} P_{2} | = | P_{1}^{'} P_{2}^{'} |$

0
Zaloguj się lub zarejestruj, by móc oceniać komentarze.
Dodaj do ulubionych

jarosinski 26-01-2021 10:04

A co do samego przekształcenia to np. zamiana x na y to jest symetria względem prostej y = x.

0
Zaloguj się lub zarejestruj, by móc oceniać komentarze.
Dodaj do ulubionych