opol 1234 wyśw. 26-01-2021 18:53

4/74 matem

Dla jakiej wartości parametru m wielomian W(x)=x^3-9x^2+26x+m spełniają warunki: x2=x1+r i x3=x2+r. Oblicz pierwiastki wielomianu i rozwiąż nierówność W(x^2+3)>/=0

Doszedłem do momentu:
x^2: -9=-3r-3x1
x: 26=2r^2+6x1r+3x1^2
x0: m=-x1^3-3x1^2r-2x1r^2

Co mam z tym zrobić? Jak skorzystać ze wzorów Viete'a i skąd je wziąć? 

matematyka matura wielomiany Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
... 27-01-2021 12:27

Właśnie zapisałeś wzory viete'a. Wzory viete'a albo należy umieć na pamięć, albo umieć wyprowadzić je. Poniżej 2 metody.

opol 27-01-2021 14:51

I co dalej z tym zrobić?

... 27-01-2021 15:08


ZioloPan 05-02-2021 19:26

Mam pytanie, w trakcie rozwiązywania układu tych 5 równań otrzymujemy równanie kwadratowe: x1^2 - 6x1 + 8 = 0

Stąd x1 = 2 lub x1 = 4

Stąd r=1 lub r=-1

I ja zapisałem coś takiego:

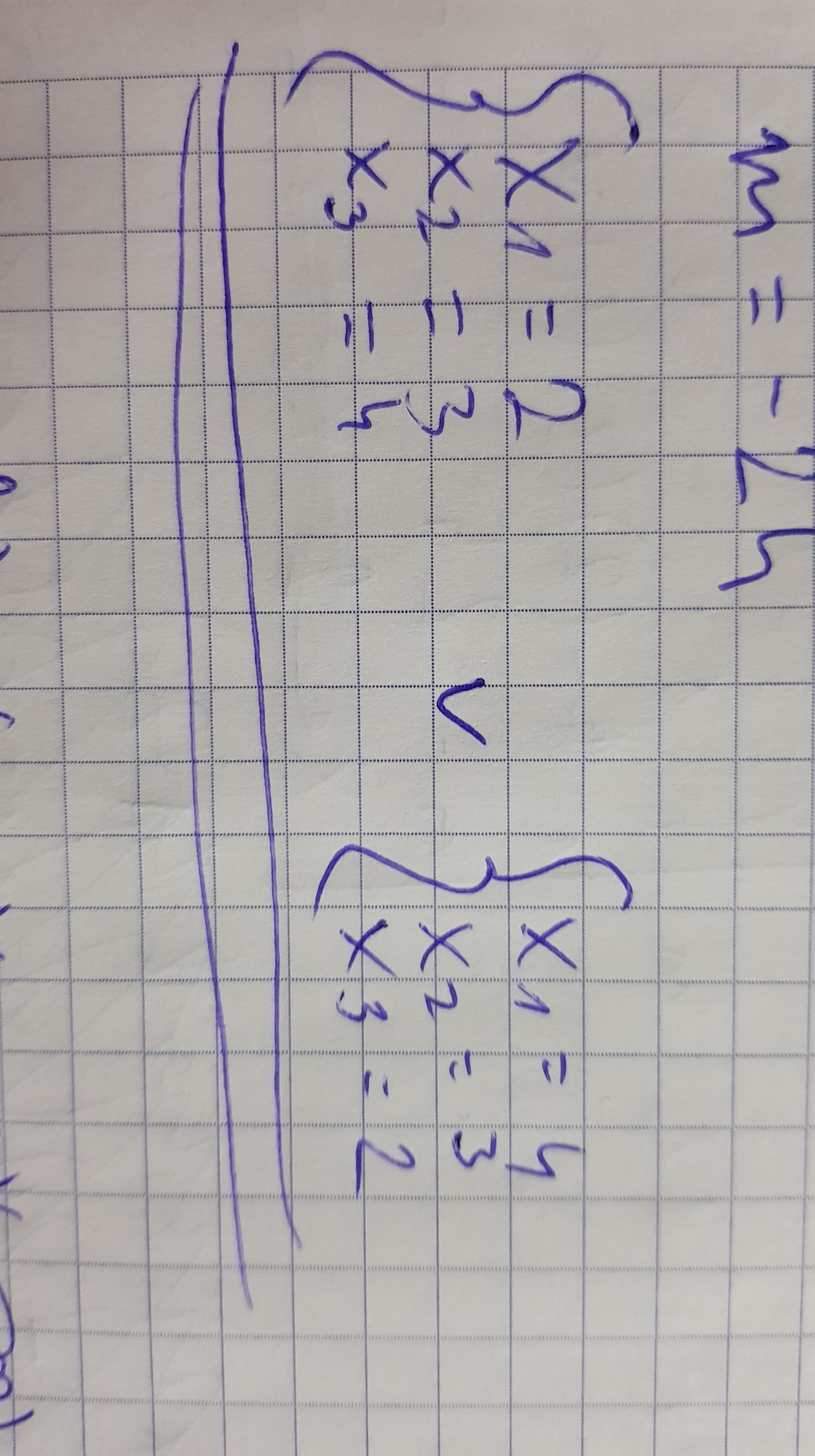
W odpowiedziach jest tylko wariant: x1 = 2 , x2 = 3, x3 = 4

Czy to co zapisałem ja to jest masło maślane? czyli czy oba warianty są równoważne?

Dlaczego w odpowiedziach jest tylko ten jeden wariant skoro druga kombinacja też spełnia warunki zadania.

... 05-02-2021 20:04

Wszystkim nam tak pwychodziło ;) Mieliśmy za zadanie obliczyć pierwiastki więc to czy x1=3 czy 3 czy 4 nie ma znaczenia ponieważ w obydwu zetawach mamy takie same pierwiastki. To co zapisałeś jest jak najbardziej poprawne :)