Mi 602 wyśw. 02-02-2021 23:26

ZZ. 105 / 205

Linia, którą kreśli punkt wykonujący niezależne drgania harmoniczne wzdłuż prostopadłych osi x i y, nazywana jest krzywą Lissajous. Krzywą można przedstawić w postaci równań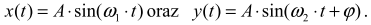

W zależności od częstości drgań ω1 i ω2 oraz przesunięcia fazowego ϕ między nimi otrzymujemy różne krzywe (patrz rysunek).

Rozwiązanie ze odpowiedzi CKE:


Należywyznaczyć sin(ω⋅t)= x i cos(ω⋅t)= y ipodstawićdojedynkitrygonometrycznej: AA

22

sin2(ω⋅t)+cos2(ω⋅t)= x + y =1, 22

AA

co prowadzi do równania okręgu x2 + y2 = A2 ,

lub wykazać, że współrzędne x i y punktu spełniają podane równanie okręgu: x2 +y2 =(A⋅sin(ω⋅t))2 +(A⋅sin(ω⋅t))2 =A2 ⋅(sin2(ω⋅t)+cos2(ω⋅t))=A2.


Dlaczego nigdzie nie uwzględniliśmy tego przesunięcia o 90 stopni, czy ja tego nie widzę?

Fizyka Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
s.gugula 04-02-2021 13:11

Przesunięcie o 90 stopni jest już uwzględnione na samym początku, a nawet już w treści zadania, jeśli bowiem do wzoru na y wstawimy fi = 90 stopni, to z sinusa robi się cosinus: y = A*sin(wt + 90) = A*cos(wt)