zad 2/88, Kurs maturalny rozszerzony
Znajdź równanie okręgu stycznego do prostych 2x+y=0 oraz 2x+y-20=0 i przechodzącego przez punkt (1,2)
Prosiłbym o rozwiązanie z wyjaśnieniem
matematyka geometria analityczna Dodaj post do ulubionych Poproś o pomoc
- 3
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tutaj starałem się inaczej, ale nie wyszło. Spróbuję jeszcze raz
https://forum.szkolamaturzystow.pl/wpis/1612556975-zadanie-domowe-19-czi-zadanie-288
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
dziękuje bardzo, za oby dwa sposoby
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
A mógłby mi ktoś pomóc skąd punkty środka okręgu wziąć.? Mam na myśli S(x, -2x+10)..
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
środek leży na prostej y = -2x + 10, stad środek ma współrzędne (x,-2x+10) bo bo s(x, f(x)), jeśli masz dostęp do lekcji to tam było dość dobrze wyjaśnione
- 2
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Dzięki Grzegorz ;) , mam dostęp i sprawdzam już :D
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czy wzór na odległość między prostymi jest w karcie wzorów? Jeśli tak to, na której stronie?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
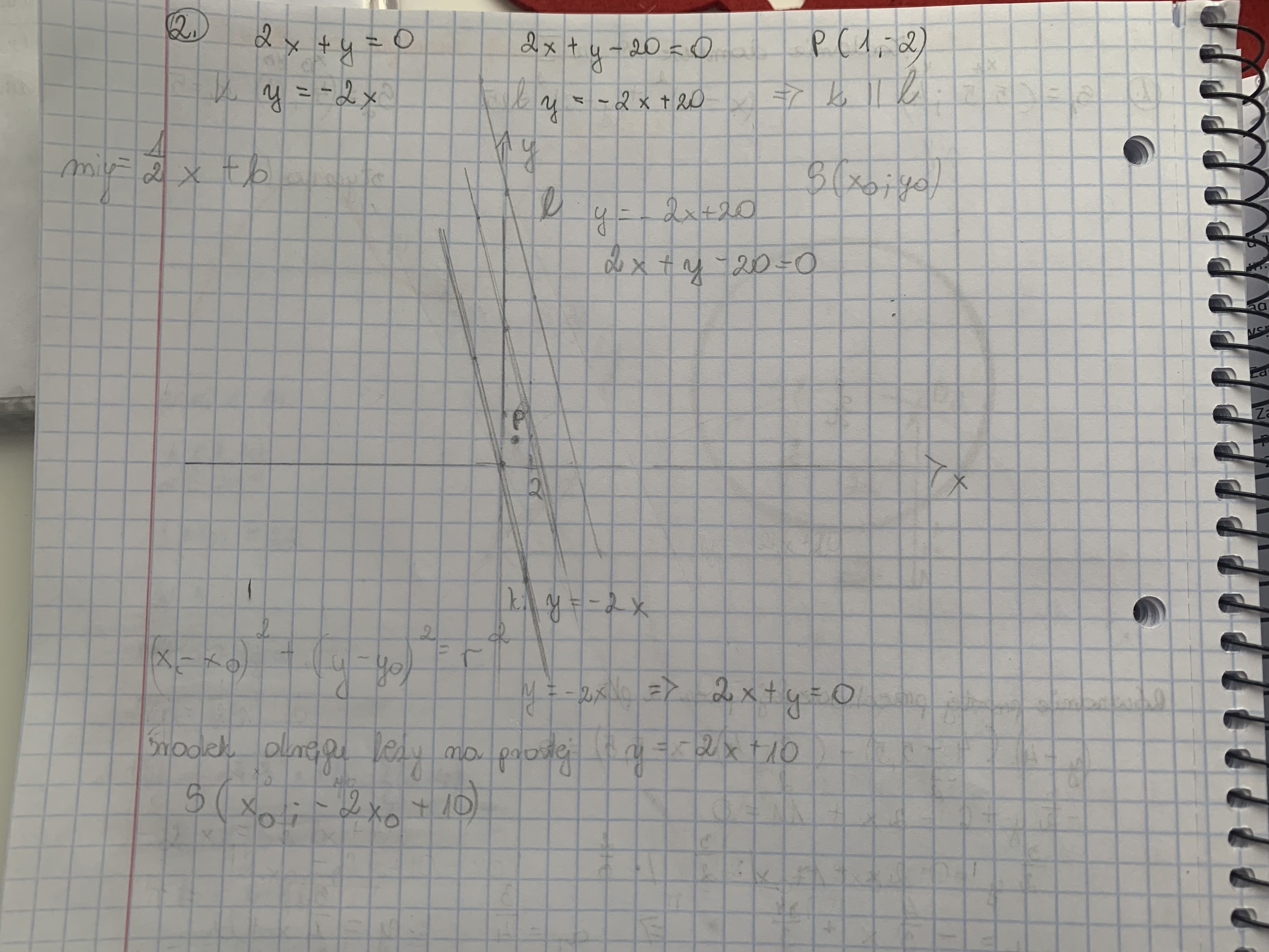
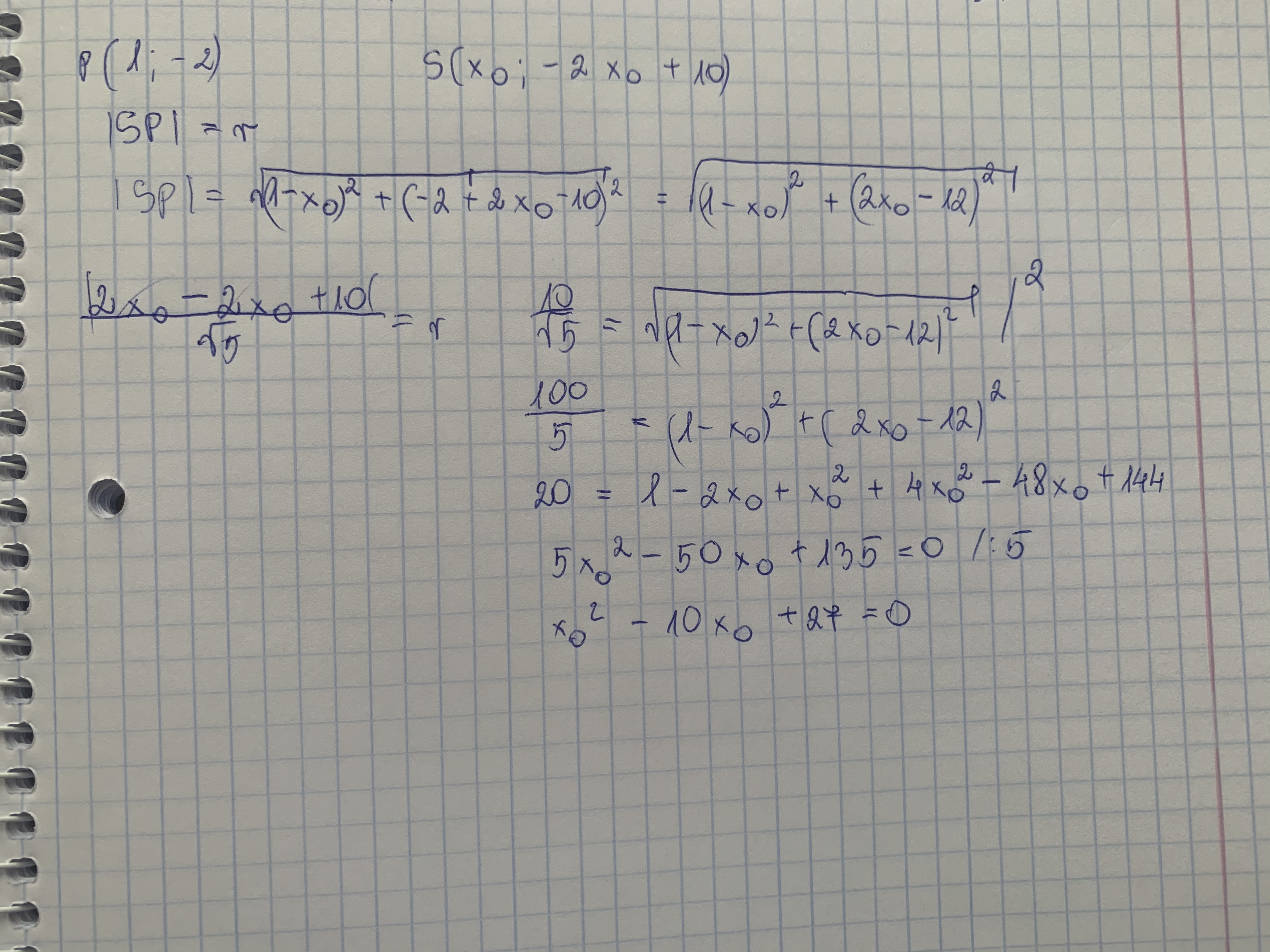
Czy można jakoś zrobić tym sposobem? Mianowicie odległość środka od punktu P to promień i odległość środka od jednej z dwóch prostych to też promień. Jednak nie wychodzą mi obliczenia.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@ <3
1 pyt) Tego wzoru nie ma w karcie. Bo nie jest on konieczny można innymi metodami to wyliczyć tylko zajmie wiecej czasu
2 pyt) Obecnie mam mało czasu ale jeśli nikt ci do wieczora nie pomoże napisz komentarz, żeby mi się wyświetliło i spróbuje pomóc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@Grzegorz.p7
Spróbowałbyś zrobić to moim sposobem?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@<3
W tym miejscu masz na pewno błąd(odległość środka od Punktu P(1;2);
Spróbuj teraz obliczyć
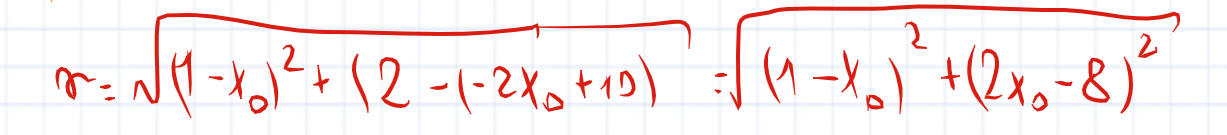
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
zauważyłem jeszcze wiecej, problem tkwi w tym ze u ciebie P=(1,-2), a w zadaniu (1,2)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych

Odległość między prostymi liczę ze wzoru: