Zadanie maturalne


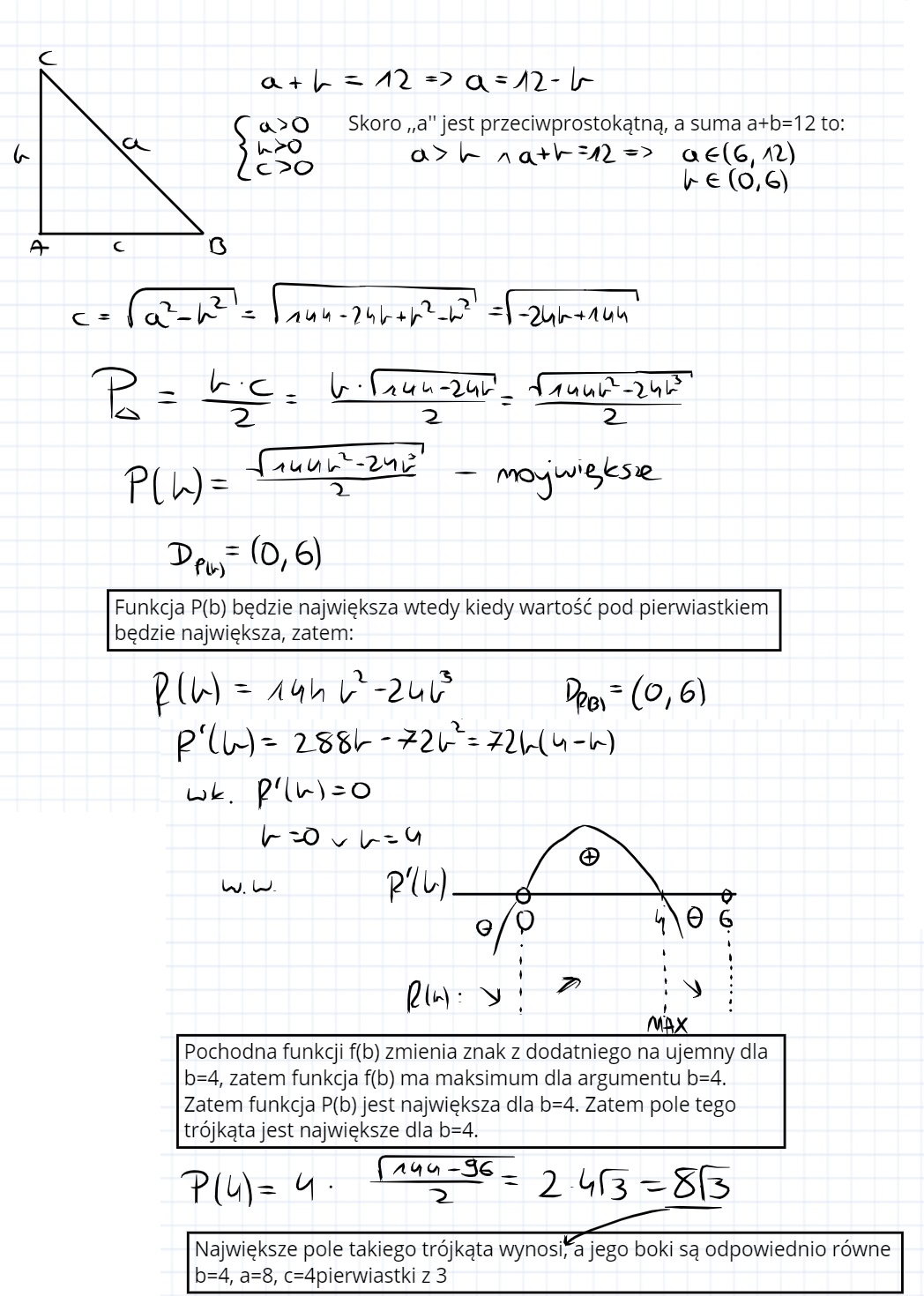
 Czy moje rozwiązanie jest poprawne? W odpowiedziach dziedzina a należy od (0;6) , mi wyszło inaczej, ale wynik i wymiary są takie same jak w odpowiedziach, ja przyjęłam trochę inne oznaczenia. Gdzie zrobiłam błąd?
Czy moje rozwiązanie jest poprawne? W odpowiedziach dziedzina a należy od (0;6) , mi wyszło inaczej, ale wynik i wymiary są takie same jak w odpowiedziach, ja przyjęłam trochę inne oznaczenia. Gdzie zrobiłam błąd?
Matematyka optymalizacja Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
1. Tak twoje rozwiązanie jest poprawne z drobnymi niuansami.
Różnica między twoją dziedziną a dziedziną z kryteriów wynika z tego, że uzależniłaś pole trójkąta od przeciwprostokątnej, a nie od przyprostokątnej. Taki sposób nie ma żadnego wpływu na rozwiązanie i jest jak najbardziej poprawny. Jeżeli uzależniasz pole trójkąta od przeciwprostokątnej to wiadome jest że dziedzina będzie inna niż jakbyś uzależniła pole od przyprostokątnej. (Jeżeli w kryteriach pisze, że dziedzina przeciwprostokątnej to (0,6) to jest to błąd w kryteriach, gdyż nie możliwym jest żeby przyprostokątna była większa od przeciwprostokątnej w trójkącie)
Chciałbym także zwrócić uwagę na moment w którym podajesz ostateczną dziedzinę. Moim zdaniem powinna zostać ona podana na samym początku. Ustalenie jej jest bardzo proste, skoro suma przeciwprostokątnej i przyprostokątnej wynosi 12, to logicznym jest , że przeciwprostokątna będzie należała do przedziału (6,12), a przyprostokątna (0,6) gdyż jak już wcześniej wspomniałem przeciwprostokątna jest zawsze większa od przyprostokątnej w trójkącie. Chodzi mi tutaj głównie o to, że twoja ostateczna dziedzina (poprawna) została wyliczona dopiero gdy zmusił cię do tego pierwiastek ( zrobiłaś założenie) natomiast gdyby nie złożyło się tak, że masz pierwiastek, mogłabyś przegapić fakt że przeciwprostokątna należy do przedziału (6,12) a nie (0,12). Co mogłoby skutkować błędną odpowiedzią.
Chciałbym zwrócić również uwagę na to, że w poleceniu pytają nie tylko o pole ale również o obliczenie i podanie długości boków, w kontekście twojego pytania jest to mało istotne, ale jeżeli pytasz o całe rozwiązanie to jest ono niepełne.
Podsumowując twoje rozwiązanie jest jak najbardziej poprawne, z drobnymi niuansami opisanymi powyżej. Poniżej przesyłam ci rozwiązanie sposobem, który prawdopodobnie jest w kryteriach do tego zadania, jest on dużo prostszy i szybszy, bo z tego co widzę dużo naliczyłaś się przy pochodnych. Może się przyda :)