opol 649 wyśw.
11-02-2021 16:33
5b/78
Dany jest ciąg określony rekurencyjnie a1=1,5 , an=2an-1
b) udowodnij, że jest to ciąg rosnący
Jak to rozwiązać?
matematyka matura ciągi Dodaj post do ulubionych Poproś o pomoc
Kliknij tutaj, aby dodać nowy komentarz.
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
opol
11-02-2021 16:40
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Emil
11-02-2021 18:40
A gdyby tak to zrobić?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
opol
11-02-2021 19:27
Nie jestem pewien bo sprawdzenie trzech pierwszych wyrazów nie daje nam uzasadnienia, że CAŁY ciąg jest rosnący.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Emil
11-02-2021 20:33
Dodać taki podpunkt i uważam, że zadanie wykonane.
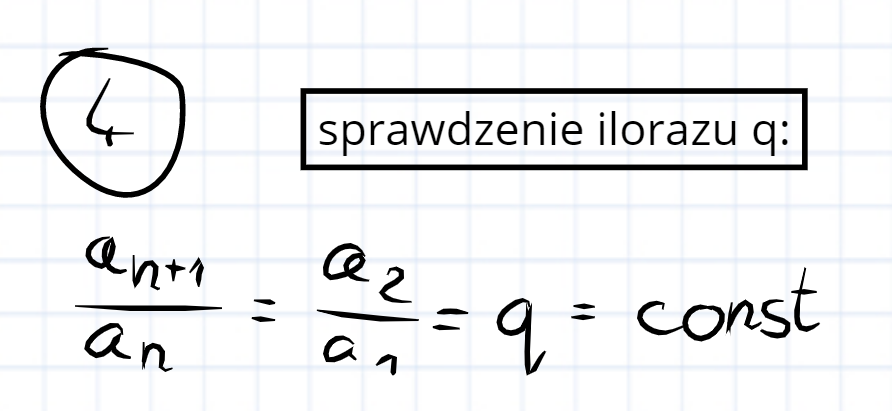
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Po prostu
an-1<an (warunek rosnącego)
podzielić przez an-1 (z prawej strony będzie 2 a z lewej 1 czyli prawdziwe?)