... 707 wyśw. 12-02-2021 20:36

Kiedy możemy odrzucić rozwiązanie a kiedy nie?

Moje pytanie dotyczy tego kiedy możemy odrzucić rozwiązanie na podstawie rysunku a kiedy nie? 
Wiem doskonale, że z rysunku nie możemy nic odczytywać a jedynie ma on nam pomóc w zrozumieniu zadania, natomiast wielokrotnie spotkałem się z taką sytuacją:
Mamy znaleźć przykładowo jeden punkt C, z równania kwadratowego wychodzą nam dwa rozwiązania, ale z rysunku widać, że jedno rozwiązanie totalnie nie ma sensu ( jest poza obszarem rozważanego problemu itd. itd.) natomiast czy nasz rysunek jest wystarczający do tego żeby napisać : ,, Dla C=(...;...) prosta nie będzie taka i owaka, dlatego odrzucamy to rozwiązanie'' czy jednak jest to informacja tylko dla nas i teraz sami musimy poprzeć odrzucenie tego rozwiązania jakimiś obliczeniami.



Na przykład chciałbym wziąć dwa zadnia z Zadania domowego 20.

Zad 1/89 Kurs maturalny rozszerzony.
Punkty A i B są punktami wspólnymi prostej y+x-5=0 oraz okręgu (x-2)^2 +(y-1)^2 =20. Na okręgu wyznacz taki punkt C, aby pole trójkąta ABC było jak największe.

Na koniec wychodzą nam dwa rozwiązania dla C, natomiast jedno zostaje odrzucone. W kryteriach nie ma żadnej wzmianki o tym dlaczego odrzucamy jedno rozwiązanie i mimo, że widać z rysunku, że wtedy trójkąt nie będzie największy, mogę tak po prostu je odrzucić? Jeżeli nie, to jak powinno wyglądać poprawne uzasadnienie w tym zadaniu? 
Czy powinienem obliczyć oba pola i wybrać jedno większe?

Kolejny przykład. 
Zad 3/89
,,Znajdź równania wspólnych stycznych do okręgów: x^2+y^2=4 oraz (x-3)^2 +y^2=1.''

Z układu równań wychodzą nam tylko 2 styczne. Z rysunku widać, że trzecia styczna będzie pionowa, poprowadzona w punkcie styczności x=2. Natomiast w kryteriach nie ma żadnego uzasadnienia co do dochodzenia dlaczego trzecią styczną jest x=2. Czy poniższy sposób uzasadnienia tego jest poprawny?

1. S1S2=r1+r2 -> Zatem te okręgi są styczne zewnętrznie. Środki okręgów leżą na osi OX zatem ich punktem przecięcia jest punkt (2,0), ponieważ okręgi są styczne zewnętrznie a ich środki leżą na osi OX to styczna do obu tych okręgów będzie miała równanie x=2.


rozwiązania odrzucanie na podstawie rysunku Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski 15-02-2021 09:37

Nie możemy odrzucać rozwiązania na podstawie rysunku. Natomiast odrzucamy na podstawie własności płynących z rys. Czyli nie pisałbym "sprzeczne (rys)", tylko raczej uzasadnienie matematyczne "sprzeczne, ponieważ (i tu matematyczne uzasadnienie)"

... 15-02-2021 13:16

Rozumiem.

Jak natomiast w zadaniu 3/89 uzasadnić, że trzecią prostą styczną jest prosta x=2.

Z układu równań wychodzą nam dwie proste l1, l2 styczne do obu okręgów, natomiast to równanie nie wypluwa nam trzeciej stycznej x=2. Jak matematycznie pokazać, że właśnie taka prosta jest trzecią styczną do obu okręgów? 
Poniżej zarys sytuacji: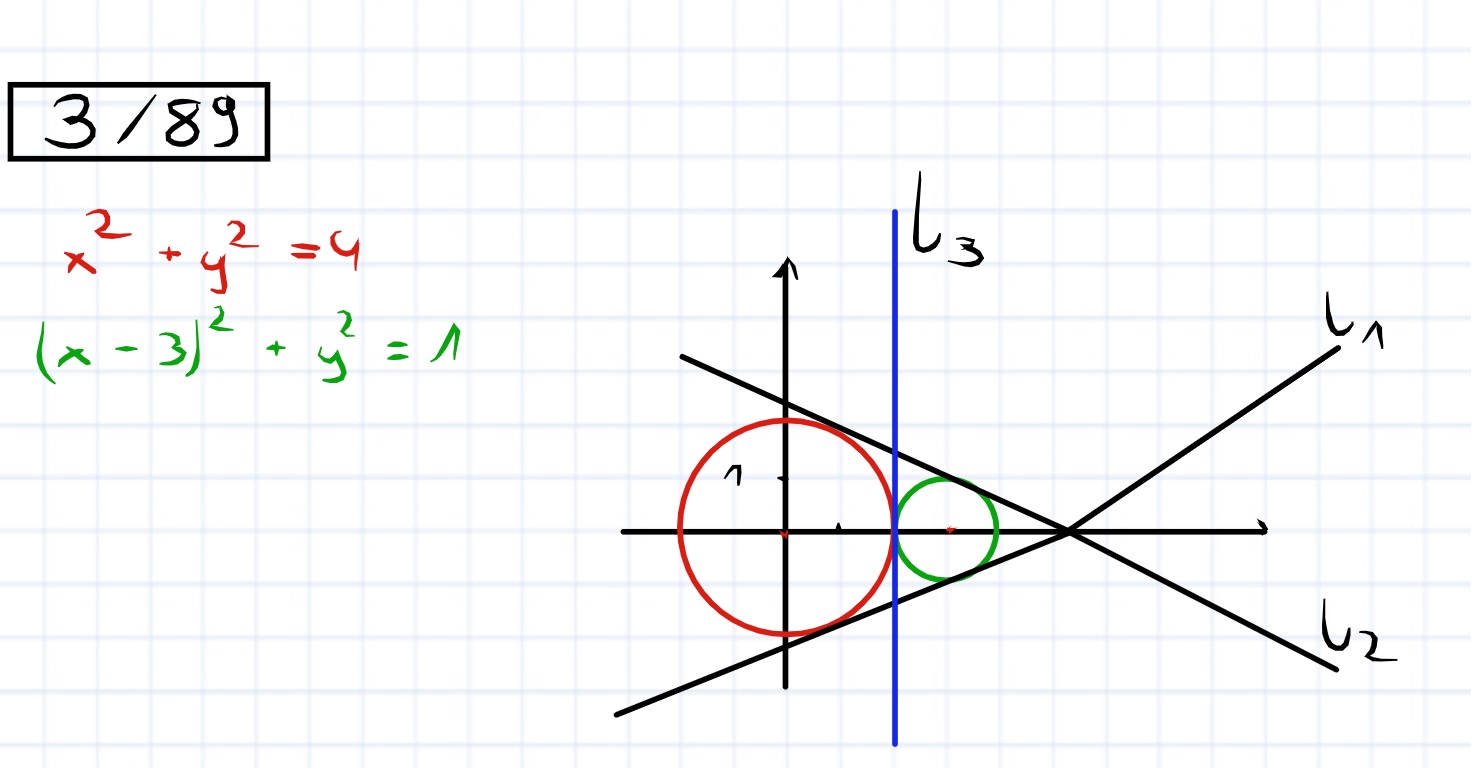

jarosinski 15-02-2021 22:54

Rozwiązanie nie musi wypływać z rachunków. Czasem metoda rachunkowa wręcz to uniemożliwia (tak jak w tym przypadku założono, że prosta jest funkcją y=ax + b). W tym przypadku najlepiej (i najkrócej) napisać, że prosta x=2 jest styczną ponieważ zachodzą dla niej warunki styczności dla obu okręgów (czyli odległość prostej od stycznej jest równa promieniowi). Wiadomo, że wiemy o tym na podstawie rysunku, ale udowadniamy to nie w oparciu o rysunek, ale matematyczne zależności