prawdopodobienstwo zadanie domowe

Czy mógłby ktoś rozpisać mi to zadanie logicznie, nie poprzez użycie wzorów ?
prawdopodobienstwo Dodaj post do ulubionych Poproś o pomoc
 Nie wiem na jakim poziomie stoisz z kombinatoryki, dlatego z takimi szczegółami, ale chyba lepiej w tą stronę niż w drugą, pozdrawiam :)
Nie wiem na jakim poziomie stoisz z kombinatoryki, dlatego z takimi szczegółami, ale chyba lepiej w tą stronę niż w drugą, pozdrawiam :)
- 25
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
czemu tą 60 zapisałeś w taki sposób, nie bardziej odpowiedni zapisem będzie ze wzoru na wariacje bez powtórzeń?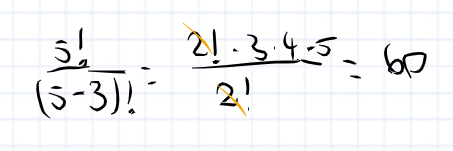
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Bez różnicy, po prostu prościej mi ułożyć sobie w głowie, ,,zajmują 3 miejsca z 5'' i można je zamieniać na 3! sposobów.
Jak wolisz wariacją bez powtórzeń, to rób wariacją bez powtórzeń. Poprawność jest jednakowa.
- 5
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Hej. Mam pytanie co prawda do zadania poprzedniego, ale jest bardzo podobne
Ja zrobilam to zadanie tak:
No i wyszło okej. Tyle że zastanawia mnie jeden fakt, dlaczego w tym zadaniu nie wybieramy np. 3 osób z 5 (w odniesieniu do drugiej ławki) a w tym co rozwiązał ... już tak?
Tutaj jakby te osoby są już dobrane do ławek a w tym co ... rozwiązał te osoby dopiero do ławek "losujemy".
Może zadanie nie na czasie ale przerabiam jeszcze raz wszystko :)
Będę mega wdzięczna za pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@Logarytm Odpowiedź jest bardzo prosta, w zadaniu 7.36 nie ma żadnego sformułowania, które jasno wskazałoby nam, że konkretne osoby chcą usiąść tak lub tak. Ludzie są rozróżnialni zatem jeżeli w poleceniu ( w tym wypadku 7.36) mamy użyte sformułowanie ,,do przedziału weszło pięć osób, trzy osoby usiadły na jednej ławce pozostałe - na drugiej (...) to musimy rozważyć każdą opcję czyli wybieramy trzy osoby z pięciu poprzez kombinacje bo dowolne trzy z pięciu bierzemy! Natomiast jeżeli spojrzymy na polecenie 7.35 to ujrzymy takie sformułowanie ,, do wagonu weszło pięć osób z których trzy chcą siedzieć przodem do kierunku a dwie tyłem " skoro trzy osoby chcą siedzieć przodem a dwie tyłem to pozwólmy im na to! Niech sobie siedzą, jeden problem z głowy! Trzy idą na jedną ławkę i dwie na drugą, nie musimy rozważać która osoba jest którą ani losować z nich.
Żeby ci to jeszcze lepiej zobrazować weźmy sobie taką sytuację:
Wiktor, Kaja, Dawid, Basia i Emilia są twoimi przyjaciółmi i rozważasz na ile sposobów możesz je usadzić na takich dwóch ławkach, jeżeli żadna z tych osób nie ma specjalnych zastrzeżeń to musisz rozważyć każdą sytuację (Kaja idzie z Dawidem i Wiktorem na jedną ławkę lub Kaja idzie z Dawidem i Basią itd. dlatego używamy kombinacji.) Natomiast jeżeli Kaja, Dawid i Wiktor powiedzieliby ci że oni razem chcą siedzieć na tej konkretnej ławce, a Emilia z Basią chcą na drugiej, to już z automatu problem masz rozwiązany i możesz przejść do ustalania ich miejsc na konkretnych ławkach.
Mam nadzieję, że temat wyczerpałem do końca :)
Pozdrawiam
- 3
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
AAA dobra. Tak jak wczoraj jeszcze nad tym myślałam to podejrzewałam że może o to chodzić, no ale teraz już mam pewność. Wielkie dzięki ... !
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Chciałabym się upewnić czy w pkt pierwszym tego zadania dobrze rozumiem wzór na kombinację 5!/3!2!. Czy w mianowniku trzy silnia oznacza permutację osób które wybraliśmy, a dwa silnia ławek, które są dostępne?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W pierwszum punkcietak jak jest to opisane mamy ilość sposobów na które możemy wybrać 3 osoby z 5.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czemu nie mnożymy jeszcze przez zamianę osób w ławkach? (3! dla pierwszej i 2! dla drugiej)
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ponieważ zostało to już uwzględnione w obliczeniach.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych