7.88 praca dom

Błąd w kryteriach 100%. 

Wynik wyszedł ci dobry. Poniżej przesyłam rozwiązanie jakby ktoś miał problem z samym rozwiązaniem :) 

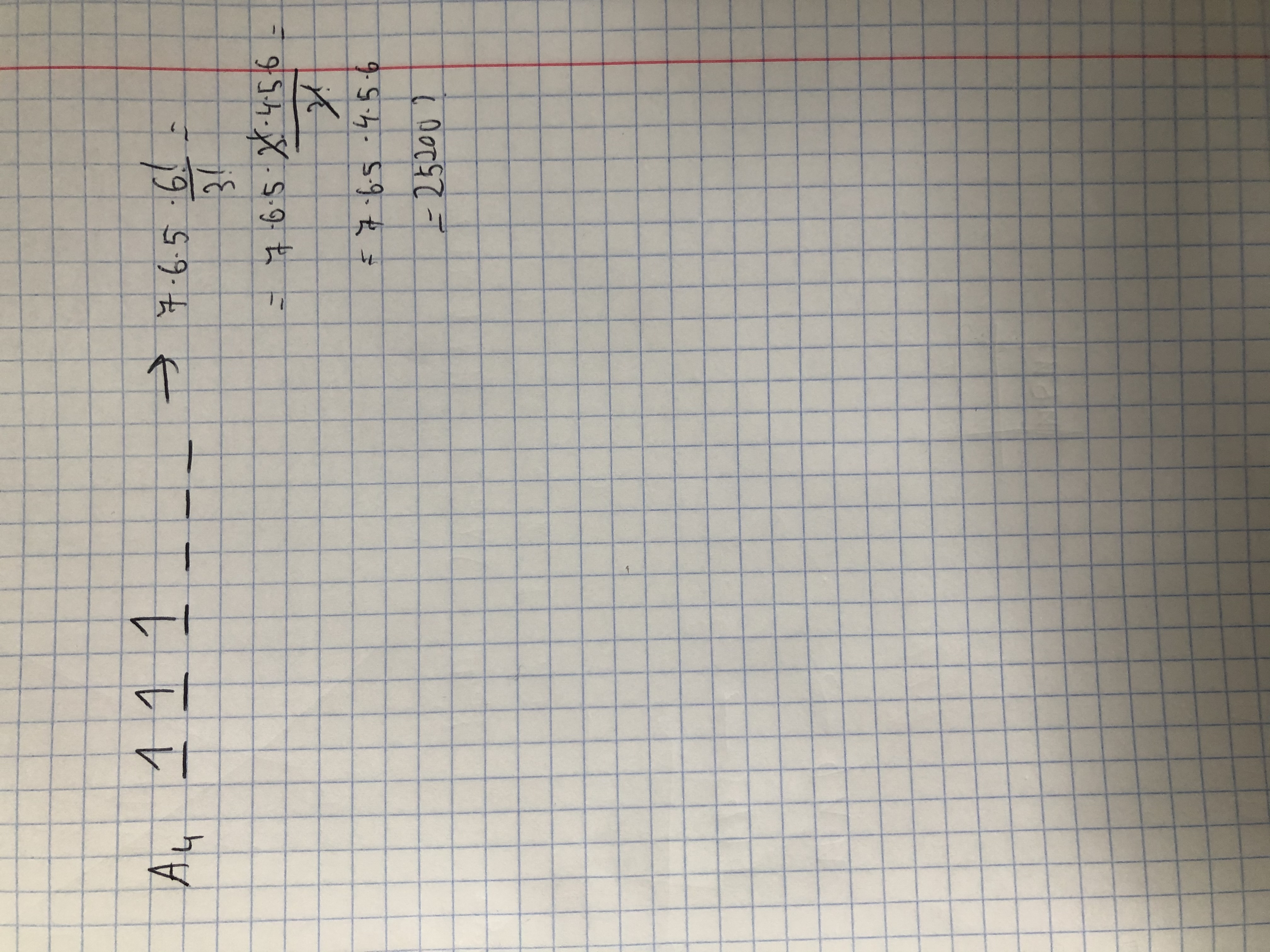Dlaczego nie możemy zrobić tego w ten sposób?

A czemu tam dałaś 6!/3!   ?

7 * 6 * 5 - wybór pozostałych

111 - potraktowałem jakbym miał je już umieszczone.

6!/3! - Na 6! - sposobów mogę je pozamieniać miejscami, a podzielone przez 3! bo "1" są nierozróżnialne.

Dlaczego takie rozumowanie jest niepoprawne ?

Co to znaczy na 6! sposobów możesz pozamieniać je miejscami a podzielone przez 3! bo są nie rozróżnialne?
Uzyskujesz za dużo sposobów.
Popatrz jeżeli masz do rozstawienia trzy "1" i masz do dyspozycji 6 miejsc to nie możesz napisać że te jedynki można rozstawić na 6! sposobów bo to jest nie prawda, mimo że później dzielisz przez 3! to dalej jest to nie prawda. Ponieważ błąd leży w ,,6!'' . W twoim rozumowaniu początkowo traktujesz jedynki jako rozróżnialne, a później dzielisz je przez możliwości ich zamiany ponieważ są nierozróżnialne - takie rozumowanie jest poprawne, tylko popatrz jeżeli założymy pierw że są nierozróżnialne to wyobraźmy sobie cyfry 1,2,3 na sześciu miejscach możemy je ułożyć nie na 6! sposobów a na 6*5*4 sposobów, wariacja bez powtórzeń, później dzielimy to przez 3! bo zakładamy że są nie rozróżnialne. W takim wypadku twoje rozwiązanie byłoby poprawne gdybyś zapisał: trzy cyfry możemy rozłożyć na 6 miejscach na 6*5*4 sposobów, a ponieważ są nierozróżnialne to dziele je przez 3! sposobów i wtedy uzyskasz poprawną odpowiedź będzie to równoznaczne kombinacji 6 po 3. Natomiast nie ma co się bawić w takie rozumowanie gdyż zachodzi tutaj prosta kombinacja. Masz 3 elementy nierozróżnialne którymi są jedynki. Masz 6 wolnych miejsc. Te trzy jedynki możemy rozstawić na 6 po 3 sposoby i koniec tematu :)

Mógłby ktoś rozpisac przez zdarzenie przeciwne? nie wiem czemu wychodzi mi całkowicie inny wynik, ktory jest niemozliwy nawet 

Dlaczego chcesz to robić przez przeciwne? Przecież dokładasz sobie jakoś 5 krotnie roboty...

Tutaj masz rozwiązanie, w tym zadaniu używanie zdarzenia przeciwnego jest bezsensowne bo tak czy siak musisz policzyć pozostałe przypadki, nie da się w tym zadaniu zebrać w kupę wszystkiego jednym obliczeniem.

dzięki, moj blad wynikal z zle policzonej omegi