W jednorodnej planecie kulistej
W jednorodnej planecie kulistej, o masie M i promieniu R, wywiercono wzdłuż promienia szyb o małym przekroju. Wykaż, że wartość siły grawitacyjnej działającej na masę próbną m umieszczoną w tym szybie jest proporcjonalna do odległości r od środka kuli, dla r<=R. Narysuj wykres siły przyciągania grawitacyjnego od r. Wiedząc, że pole pod wykresem siły od przemieszczenia jest równe wykonanej pracy, oblicz pracę wykonaną nad ciałem podczas jego przemieszczenia się w szybie z powierzchni planety na głębokość h. Na tej podstawie zdefiniuj energię potencjalną ciała liczoną względem powierzchni kuli . Narysuj wykres tak zdefiniowanej energii potencjalnej od głębokości. Korzystając z zasady zachowania energii dla pola grawitacyjnego, oblicz prędkość ciała spadającego swobodnie w zależności od głębokości szybu. Otrzymane wzory zastosuj do obliczenia prędkości upadku ciała na dno szybu o głębokości h=1km znajdującego się w Ziemi. Przyjmij dla Ziemi: gz=9,81m/s^2 i Rz=6,38 *10^6m. Porównaj ten wynik z prędkością swobodnego spadku w jednorodnym polu grawitacyjnym o wartości gz. Zaniedbaj ruch obrotowy Ziemi i siły oporu powietrza.
Jak powinno się rozwiązać to zadanie? Nie za bardzo wiem od czego zacząć.
Fizyka grawitacja i kosmologia Dodaj post do ulubionych Poproś o pomoc
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Wszystko jasne oprócz tego pola pod wykresem, dlaczego akurat trapez i jak narysować wykres F(h), aby powstała wspomniana figura. Nie rozumiem także skąd się bierze ta końcówka przy wzorze pracy: h^2 i 2R^3
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Trapez, ponieważ mamy taki wykres F(r):
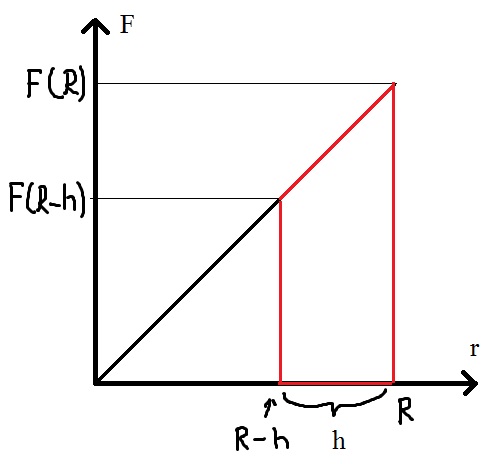
Ta praca W to będzie pole tego trapezu, czyli 0,5*h*(F(R) + F(R-h)), po jej obliczeniu będziemy mieli własnie takie wyrażenie jak napisałem powyżej. Jeśli teraz będziemy chcieli wyznaczyć energię potencjalną względem powierzchni (czyli rozumiem to tak, że przyjmujemy, że na powierzchni ta energia jest zerowa, a im głębiej tym ta energia potencjalna musi maleć), to wystarczy zapisać, że Ep = -W. Wyjdzie więc, że ta energia potencjalna będzie funkcją kwadratową głębokości h, będzie przyjmowała wartość zero dla h = 0 i osiągnie minimum dla h = R (czyli środek planety). Drugie miejsce zerowe będzie dla h = 2R, będzie to odpowiadało sytuacji, gdy ciało przejdzie przez środek planety i znajdzie się na jej powierzchni po drugiej stronie.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W=((GMm/R^2+GMm/(R-h)^2)*h)/2 czyli będzie coś takiego?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Nie ponieważ siła F(r) nie przyjmuje postaci GMm/r^2, ale inną wynikającą z tego wyprowadzenia, które zawarte jest w linku, który podesłałem w pierwszym moim poście. Ma ona postać: F(r) = (4/3)*pi*ro*G*m*r, ale za ro (gęstość) wstawiamy po prostu masę planety przez jej objętość, czyli ro = M/((4/3)*pi*R^3). Ostatecznie wychodzi, że siłą ma następującą postać: F(r) = GMm*r/R^3. I teraz do tego wzoru podstawiamy R, a następnie R - h, żeby dostać odpowiednio F(R) i F(R-h), które dadzą nam pole tego trapezu, czyli pracę W. Wyjdzie ona taka jak w moim wcześniejszym poście ;)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Trzeba na początku udowodnić, że siła grawitacji działająca na masę próbną wewnątrz kuli jest wprost proporcjonalna do r. W tym celu odsyłam do poniższego linka gdzie jest to fajnie ukazane: http://ilf.fizyka.pw.edu.pl/podrecznik/2/5/3
Wykres siły przyciągania w zależności od r będzie po prostu liniowy.
Pole pod wykresem przy przemieszczaniu się w szybie z powierzchni planety na głębokość h to będzie pole trapezu, o ile nie pomyliłem się w obliczeniach, które tu na szybko robię, powinno to wyjść W = GMmh/R^2 - GMm*h^2/2R^3. Będzie to jednocześnie różnica energii potencjalnej ciała na powierzchni planety i na głębokości h -> stąd uzyskujemy wzór na energie potencjalną tego ciała "względem powierzchni". No i podczas spadku ciała w szybie jego energia potencjalna zostaje zamieniona na energię kinetyczną, czyli mv^2/2, skąd można wyliczyć prędkość takiego ciała w zależności od głębokości.
Oczywiście to zadanie jest trudne, więc w razie dalszych niejasności pytaj śmiało :)