ADRYAN11 1427 wyśw. 24-02-2021 20:06

2/90 jaki znak w nierówności z wartościa bezwzględna

Rozwiaż nierówność: x^4 +13 >= |13x^3 +x| 


Pogubiłem się trochę w tym, jaki dajemy znak przy rozbijaniu nierówności z wartościa bezwzględna. W odpowiedziach do tego zadania sumujemy oba rozwiazania, więc jest znak lub, ale zgodnie z ta definicja powinno chyba być "i" 


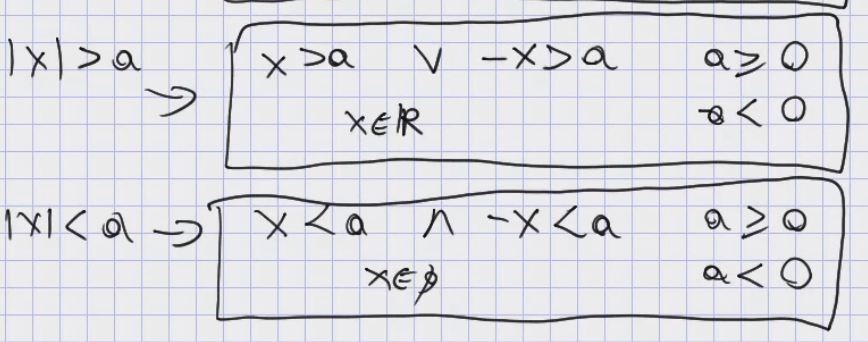
Robiac zgodnie z zasada, że obracamy znak nierówności o 90 stopni w prawo na poczatku dałem spójnik "lub" (opcja ozn. jako 1), ale po przekształceniu nierówności tak, by wartość bezwzględna była po lewej stronie zasada ta daje nam spójnik "i" (opcja 2) 


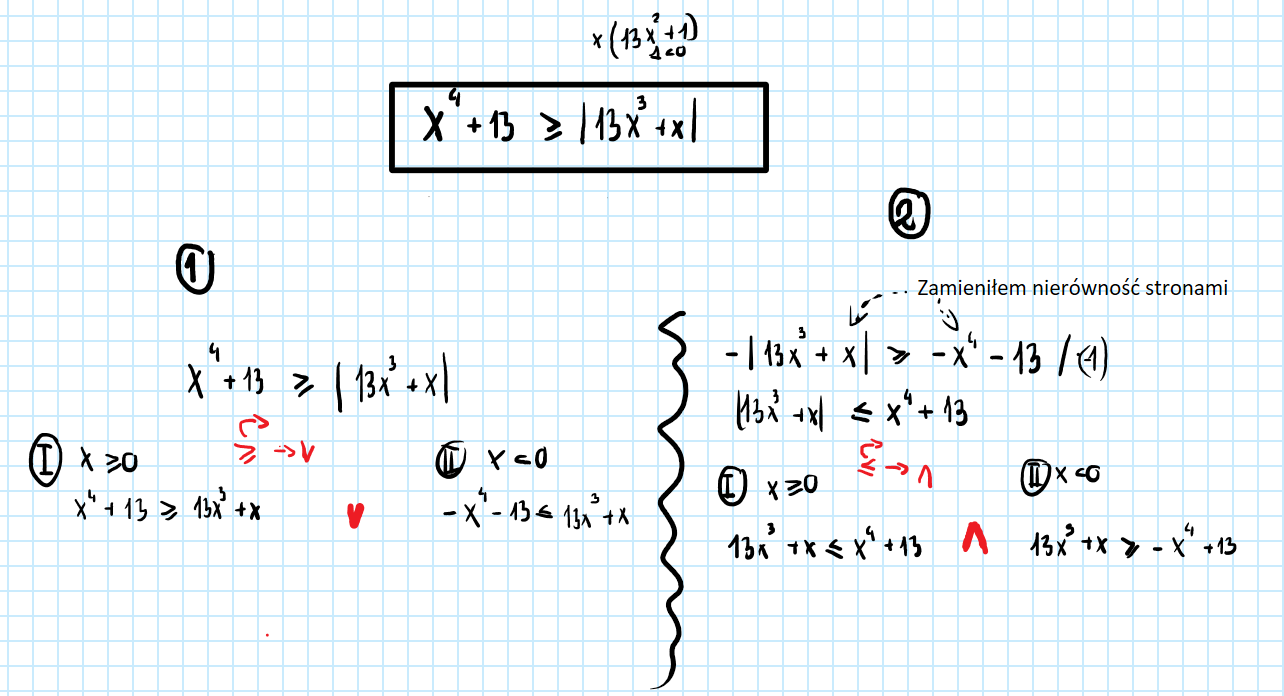
wartość bezwzględna spójniki Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
Onomatopeja 24-02-2021 20:49

Zauważ, co się dzieje gdy wstawimy tam spójnik "i". Z samych warunków (x>=0 x<0) wynikało by, że równanie nie ma rozwiązań a jednak np. "0" spełnia to równanie. 

Wniosek jest taki, że gdy mamy niewiadome poza wartością bezwzględną lub inną wartością (czyli gdy musimy postawić jakiś warunek do zadania) nie możemy fizycznie postawić spójnika "i" pomiędzy kolejnymi warunkami (czyli pomiędzy np x>=0 i x<0), gdyż prowadzi to do często oczywistej sprzeczności. Musimy więc postawić spójnik "lub".

Mam nadzieję, że pomogłem. Powodzenia!