pj20 1480 wyśw.
01-03-2021 18:02
nowa era arkusz nr 2 rozszerzony zadanie 5/60
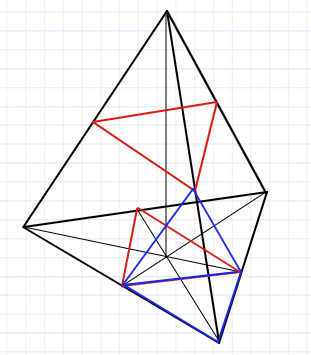
Objętość wielościanu, którego wierzchołkami są środki krawędzi dowolnego czworościanu o objętości V, jest równa:
| 1 | ||
A. | V | |
| 8 |
|
| 1 | ||
B. | V | |
| 4 |
|
| 1 | ||
C. | V | |
| 3 |
|
| 1 | ||
D. | V | |
| 2 |
Proszę o pomoc z tym zadaniem i wytłumaczenie.
matematyka Dodaj post do ulubionych Poproś o pomoc
Kliknij tutaj, aby dodać nowy komentarz.
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski
04-03-2021 08:45
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Najpierw należy określić z jaką bryłą mamy do czynienia. Powstała bryła ma odjęte cztery małe czworościany względem tego początkowego (rys - niebieskie). Te niebieskie czworościany są podobne do dużego w skali k = 1/2. Stosunek objętości wynosi k^3. Zatem jeden niebieski czworościan ma objętość V/8. Cztery mają objętość V/2. Zatem powstała bryła ma objętość V - V/2 = V/2. Odp: D.