... 646 wyśw. 08-03-2021 16:11

Wykres pochodnej - pytanie.

Czy wykres pochodnej powinien być narysowany w dziedzinie pierwotnej funkcji?

Chodzi mi o to, że na lekcjach rysowaliśmy wykres pochodnej w całej dziedzinie, później zaznaczaliśmy dziedzinę oraz rozpatrywaliśmy w dziedzinie funkcje właściwą.

Natomiast w każdych kryteriach jakie udało mi się przepatrzeć, przy obliczeniu pochodnej jest napisane przykładowo:

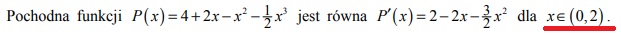
Pytanie 1) Zatem czy może być potraktowane jako błąd narysowanie pochodnej w całej dziedzinie, mimo że dziedzina funkcji jest inna.

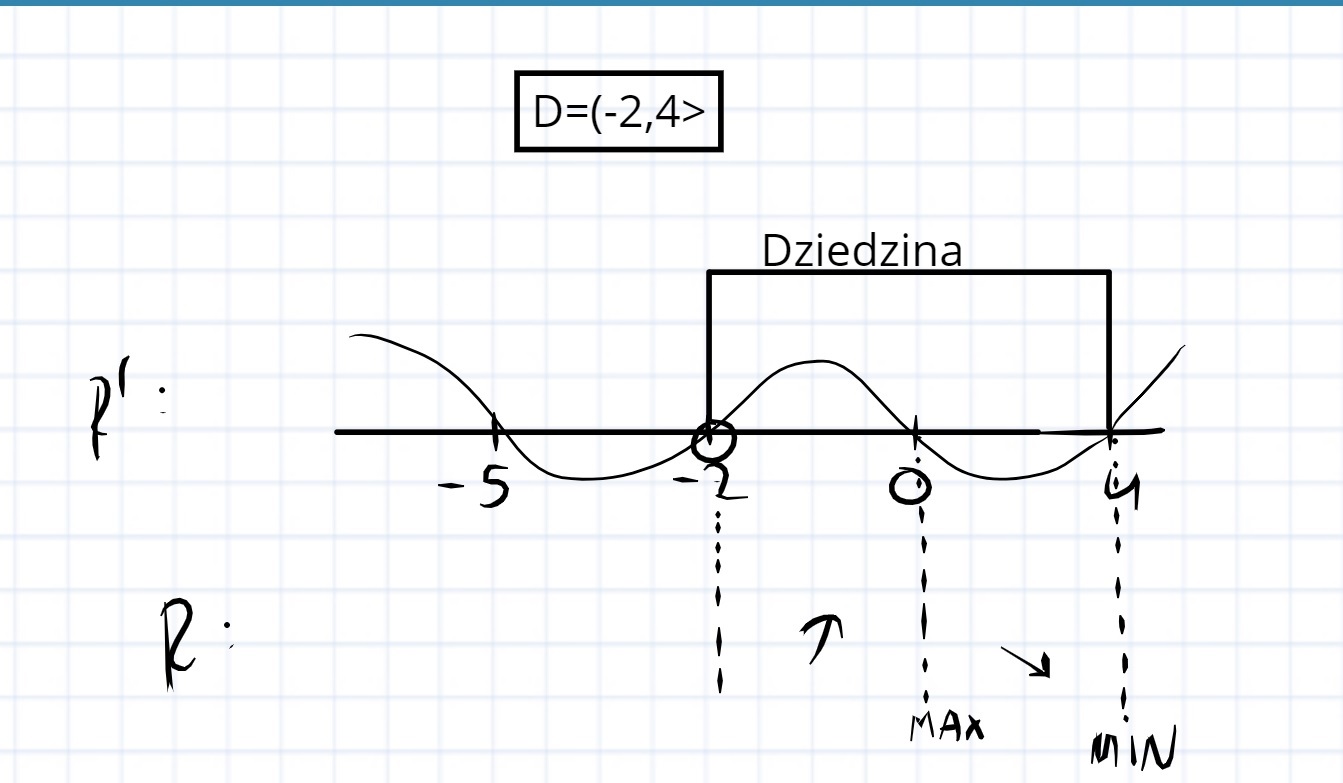
Pytanie 2) Jeżeli odpowiedź na pytanie 1) jest taka, że można tak robić to jak najlepiej zaznaczyć dziedzinę w której rozpatrujemy. Czy takie coś będzie ok?:



pochodna wykres pytanie techniczne Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
jarosinski 10-03-2021 09:49

1) można tak zrobić, nie widzę powodu dla którego miałoby to być potraktowane jako błąd jeśli tylko dziedzina jest wyraźnie zaznaczona i jeśli rozpatrujesz pochodną tylko w tym przedziale 

2) jest ok; oczywiście można też narysować pochodną tylko w samej dziedzinie 

... 11-03-2021 20:18

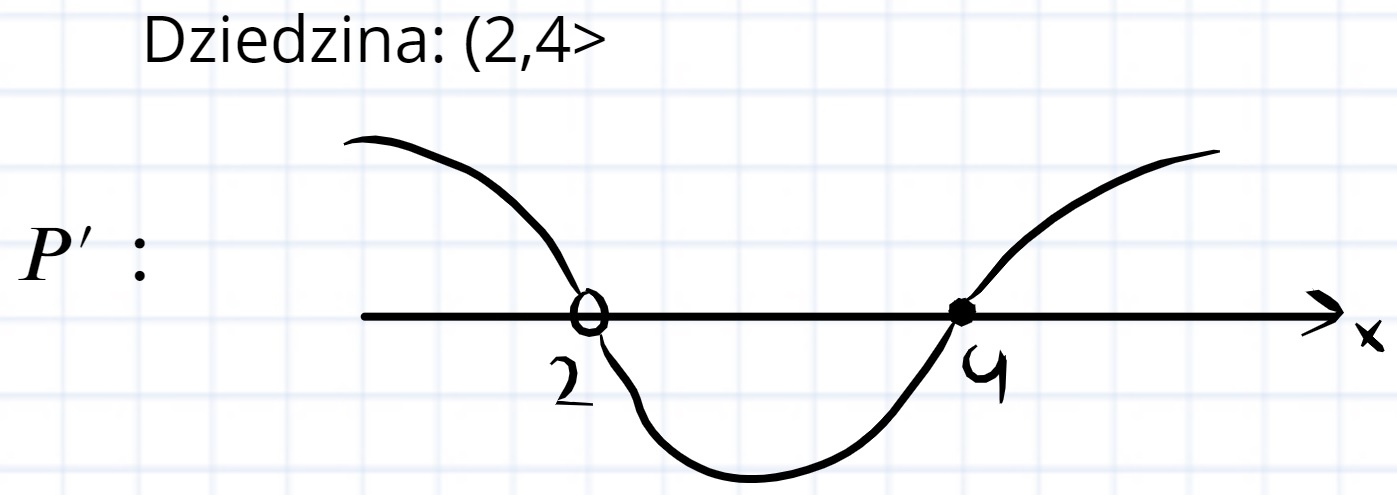
A czy w takim przypadku przy optymalizacji funkcji, jeżeli dziedziną jest przedział (2,4> uznajemy czwórkę za minimum lokalne? Bo z jednej strony zachodzi zmiana znaku a z drugiej strony przedział to (2,4> zatem za czwórką już "nic nie ma".

jarosinski 11-03-2021 22:35

Możemy uznać to za ekstremum lokalne w kontekście jego lewostronnego otoczenia (prawostronne nie istnieje). 

... 11-03-2021 22:44

Zatem w zadaniu zamkniętym w pytaniu o ilość ekstremów w przedziale należałoby uwzględnić to jako minimum lokalne?

jarosinski 12-03-2021 08:52

Ciężko stwierdzić, troszkę się to kłóci z definicją ekstremum lokalnego (chodzi o przedział otwarty):

Funkcja f(x) przyjmuje w punkcie x0 maksimum lokalne (odpowiednio: minimum lokalne), jeśli w pewnym otwartym otoczeniu tego punktu (np. w pewnym przedziale otwartym) funkcja nigdzie nie ma wartości większych (odpowiednio: mniejszych).

Natomiast na maturze na pewno nie dadzą takiego pytania.

Ps. Do ekstremów globalnych oczywiście to wliczamy