5/91
Dany jest kwadrat ABCD o boku 1 w którego wpisana jest ćwierć okręgu (rys.). Ile wynosi minimalna długość odcinka EF stycznego do okręgu?
Jak wykazać że trójkaty EBG oraz BFG sa przystajace? czy GB to dwusieczna, i jeśli tak to dlaczego?
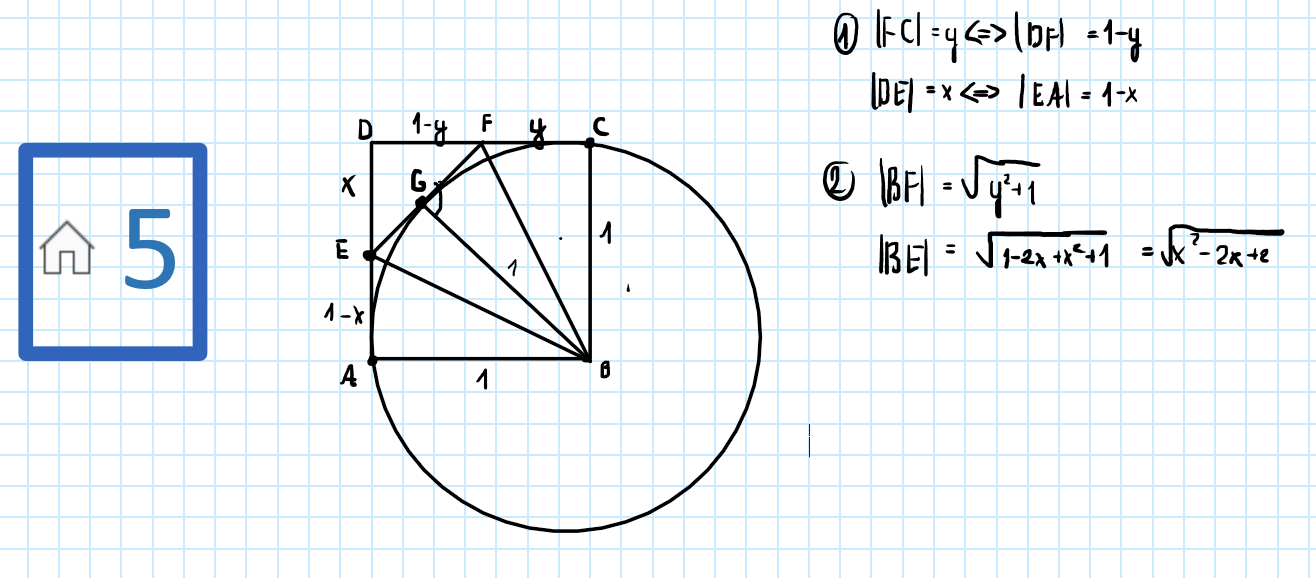
optymalizacja Dodaj post do ulubionych Poproś o pomoc
Nie rozumiem 2 pierwszych równań, czy mógłbyś rozpisać?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Najpierw wyznaczam sobie zależności między kątami sprowadzając wsyztsko do alfy, później liczyłem obwód (wyszedł równy 2 więc nie jest zależy od niewiadomej x i/lub y). Z tego wynika wniosek w żółtej ramce.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak wiem wiem, dalej już ogarniam, tylko chodzi mi właśnie o moment gdzie uzależniasz katy gamma i delta od alfa i beta. Skad biora się te dwa równania? 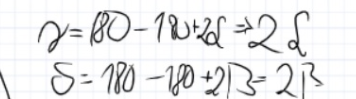
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Jest tak dlatego że, AEGB jest deltoidem tak samo jak BGFC. Suma kątów przy krawędzi kwadratu musi być równa 180, dwa kąty które tam znasz mają miarę 90-alfa oraz 90-alfa. Stąd ta równość, analogicznie do tego rozpisałem tę drugą nierówność.
(Mam nadzieję, że teraz dobrze wytłumaczyłem)
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
