Jakub 575 wyśw. 11-03-2021 15:47

568 Kiełbasa

Suma długosci wszystkich krawędzi podstawy i wysokość ostroslupa prawidlowego trojkatnego wynosi 18 cm. Zbadaj, jaką wysokość powinien mieć ten ostrosłup, aby jego objętośc była największa. Oblicz tę objętość.

Czy odpowiedzi do tego zadania są poprawne? Pole wyszło mi takie samo. Natomiast wysokość wyliczyłem na 6 i bok na 4, a w odpowiedziach wysokość wynosi 2. Ktoś może rozwiązał i miał podobny problem?

Odpowiedzi Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
Drzazgusia 11-03-2021 16:02

Witam, również wysokość wyszła mi równa 6 a bok 4. Pozdrawiam

Emil 14-03-2021 22:59


Cześć, pomógłby mi ktoś znaleźć tutaj błąd?

... 14-03-2021 23:27

Nie możesz czegoś takiego zrobić.
Jeżeli masz ułamek w którym masz liczbę to masz dwie możliwości. 
1) Wykorzystać klasyczny wzór na pochodną ilorazu ( nie polecam jak masz tylko liczbę w mianowniku) 
2) Rozbić na dwa ułamki i klasycznie policzyć pochodną.

Emil 15-03-2021 00:21

Dałbyś radę rozpisać to mi? Zawsze tak robiłem i w poprzednich zadaniach wszystko mi wychodziło, no i wydaje mi się ze jak uzywam wzoru na pochodna ilorazu to pochodna góry pomnożona przez mianownik (zmienna ‚x’) i później jest minus „zero” i kwadrat mianownika i tego kwadratu nie można skrócić z tym czynnikiem (zmienna ‚x’) w tej pierwszej części ? 

edit 1: to mam na myśli:

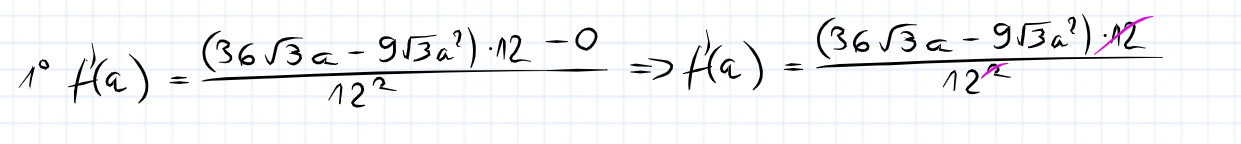
edit 2: znalazłem błąd przy wyciąganiu przed nawias