2/92 cz. II
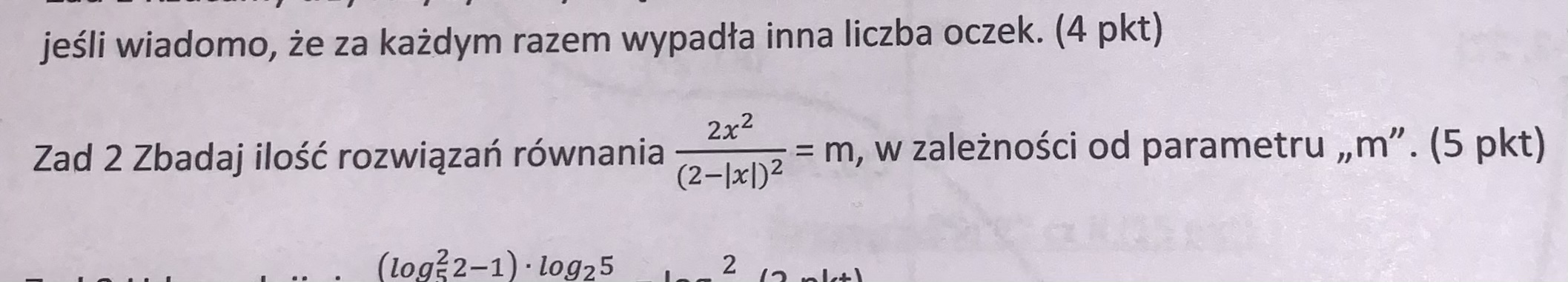
Bardzo proszę o rozwiązanie tego zadania krok po kroku
Parametr m Dodaj post do ulubionych Poproś o pomoc
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Czy mógłby ktoś wyliczyć asymptoty? Jakoś ciągle wychodzi mi tylko pozioma.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
@Lucy asymptota pionowa będzie w 2 i w -2 wychodzi to z dziedziny funkcji
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tylko czy w takim przypadku jak coś wypadało z dziedziny nie trzeba było dla upewnienia obliczyć granic?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Można ale w tym przypadku nie jest to konieczne, jeśli chcesz policzyć te granice liczysz granice przy x dążącym do 2 z lewej i z prawej strony (tak samo dla -2), dla obu wyjdzie ci, że te granice są w nieskończoności.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Tak tylko mnie wyszło, że z obu stron dążą do + nieskończoności, a w takim przypadku raczej asymptota nie istnieje, chyba że coś źle policzyłam.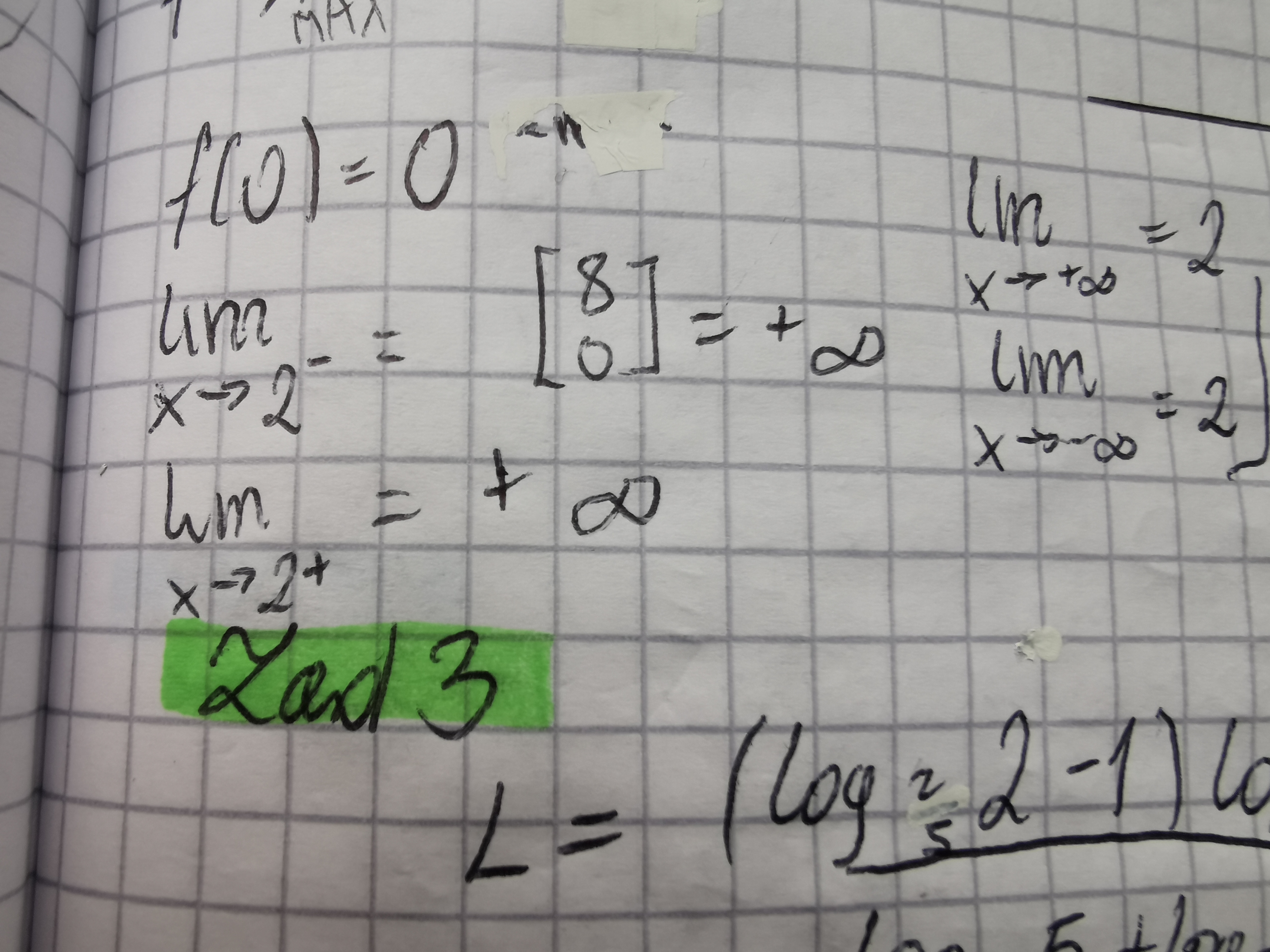 
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Masz rację dąży w obu przypadkach do plus nieskończoności ale czemu asymptota miałaby nie istnieć? Chodzi ci teraz o asymptotę pionowa czy poziomą?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Chodzi mi o pionowe asymptoty.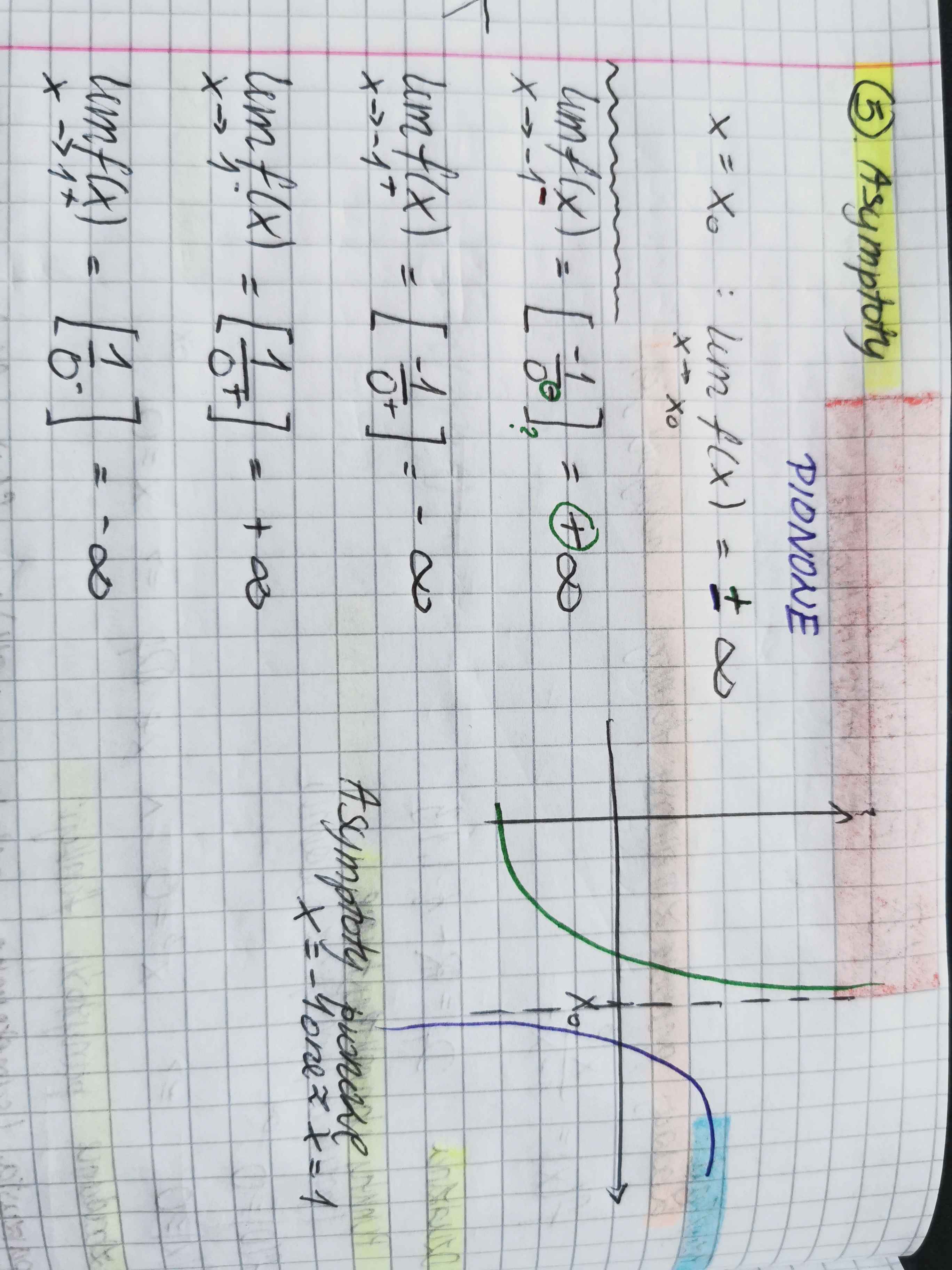 
Myślałam, że asymptota istnieje tylko i wyłącznie gdy spełnia ten warunek z granicą.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
W odpowiedziach też to wymagają, tylko że mnie nie wychodzi jakoś.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
ale ten warunek z granicą jest przecież spełniony. Będzie po prostu wyglądać tak jak na tym zdjęciu co wysłałaś.
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Ale skoro granicę wyszły obustronnie +nies to czy warunek jest spełniony? To nie jest źle?
- 0
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
nie, nie jest źle, takie granice jak najbardziej istnieją.
- 1
- Zaloguj się lub zarejestruj, by móc oceniać komentarze.
- Dodaj do ulubionych
Masz liczbę dodatnią przez liczbę dodatnią, z czego wynika, że m nie może być liczbą ujemną, żeby m było równe zero to x również musi być równe zero więc jest takie tylko jedno rozwiązanie. Następnie liczysz sobie granicę przy nieskończoności i minus nieskończoności, wyjdzie "2". Skoro granica jest równa dwa liczysz liczbę rozwiązań dla m należącego do przedziału (0, 2>, np.: dla 1. Wyjdzie ci wtedy, że są dwa takie rozwiązania. Następnie liczysz liczbę rozwiązań dla m należącego od (2, nieskończoności), np.: możesz podstawić za m "5", wyjdzie ci wtedy, że są 4 takie rozwiązania.
Więc
dla m należącego (-nieskończoności, 0), zero rozwiązań
dla m równego {0}, jedno rozwiązanie
dla m należącego (0, 2> dwa rozwiązania
dla m należącego (2, nieskończoności) cztery rozwiązania
Można również narysować funkcję i odczytać wartości parametru m z jej wykresu, ale to będzie mniej pewne niż liczenie.