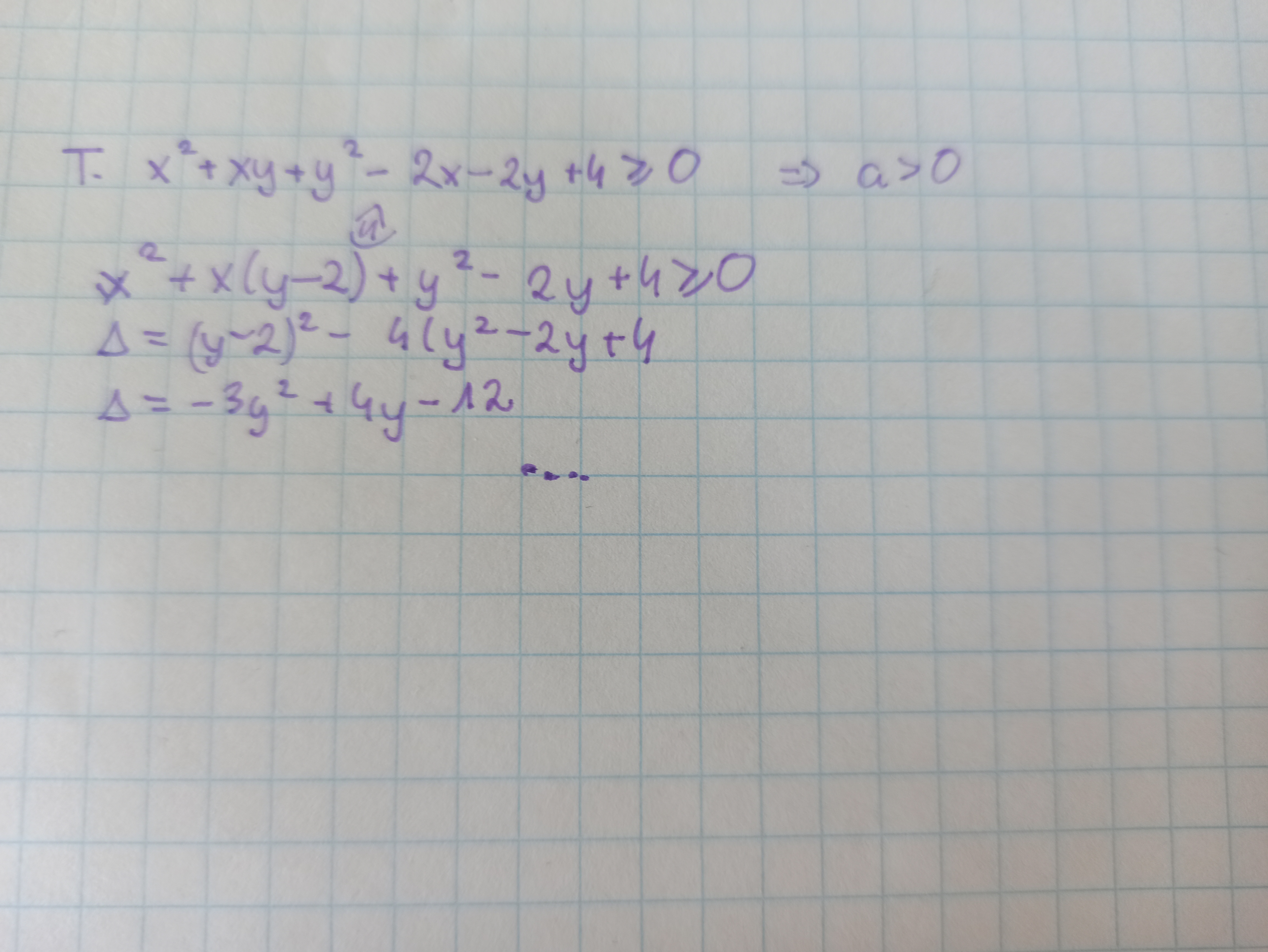mbajolek 1250 wyśw. 15-03-2021 09:47

Zadanie na dowodzenie

Uzasadnij, że dla dowolnych liczb rzeczywistych x,y prawdziwa jest nierówność:

x^2 + xy + y^2 ≥ 2x + 2y - 4

Próbowałam zrobić to zadanie sposobem z funkcją kwadratową i parametrem, ale nie wychodził mi zaden wzór skróconego mnożenia żeby udowodnić, że delta jest mniejsza od 0. 

dowodzenie nierówności Dodaj post do ulubionych Poproś o pomoc
Zaloguj się lub zarejestruj, by móc dodawać komentarze.
mbajolek 15-03-2021 09:48

Na tym sie zatrzymałam:

... 15-03-2021 10:26
Zdjęcie się nie wyświetla. Prześlij jeszcze raz albo przepisz polecenie. 
mbajolek 15-03-2021 10:39

Juz jest :)

Drzazgusia 15-03-2021 10:57

Witam, wystarczy teraz wyliczyć deltę delty, która wychodzi -560, a=-3 ( czyli mniejsze od 0) czuli cała funkcja : -3y^2+4y-12 znajduje się pod osia ox czyli delta pierwotnej funkcji zawsze jest mniejsza od 0

... 15-03-2021 11:02


... 15-03-2021 11:41

Można jeszcze tak :)